题目内容
19.已知cot(sinθ)•tan(cosθ)>0,角θ是第几象限的角一,三.分析 由题意知:cot(sinθ)>0,tan(cosθ)>0或cot(sinθ)<0,tan(cosθ)<0,可得$\left\{\begin{array}{l}{0<sinθ<1}\\{0<cosθ<1}\end{array}\right.$或$\left\{\begin{array}{l}{-1<sinθ<0}\\{-1<cosθ<0}\end{array}\right.$,从而即可得出答案.
解答 解:由题意知:cot(sinθ)>0,tan(cosθ)>0或cot(sinθ)<0,tan(cosθ)<0,
∴$\left\{\begin{array}{l}{0<sinθ<1}\\{0<cosθ<1}\end{array}\right.$或$\left\{\begin{array}{l}{-1<sinθ<0}\\{-1<cosθ<0}\end{array}\right.$,
∴θ为第一或第三象限角.
故答案为:一,三.
点评 本题考查了任意角的三角函数的定义及象限角,关键是掌握分类讨论的思想,属于基础题.

练习册系列答案
相关题目
9.已知平面向量$\overrightarrow a$=(0,-1),$\overrightarrow b$=(1,1),|λ$\overrightarrow a$+$\overrightarrow b$|=$\sqrt{5}$,则λ的值为( )
| A. | 3 | B. | 2 | C. | 3或-1 | D. | 2或-1 |
10.若直线x+(1+m)y+m-2=0与直线mx+2y+6=0平行,则实数m的值是( )
| A. | -2 | B. | 1 | C. | -2或1 | D. | m的值不存在 |
7.已知不等式|x-2|<3的解集为A,函数y=ln(1-x)的定义域为B,则图中阴影部分表示的集合为( )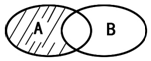

| A. | {x∈R|-1<x<1} | B. | {x∈R|1≤x<5} | C. | {x∈R|1<x<5} | D. | {x∈R|x≥1} |
14.若满足∠A=30°,BC=10的△ABC恰好有不同的两个,则边AB长的取值范围为( )
| A. | (5,10) | B. | (10,20) | C. | [20,+∞) | D. | (5,10)∪[20,+∞) |
9.设函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+1,x≤1}\\{2{x}^{-1},x>1}\end{array}\right.$,则f(f(3))的值是( )
| A. | $\frac{1}{5}$ | B. | 3 | C. | $\frac{2}{3}$ | D. | $\frac{13}{9}$ |