题目内容
7．已知不等式|x-2|＜3的解集为A，函数y=ln（1-x）的定义域为B，则图中阴影部分表示的集合为（ ）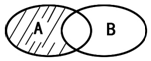
| A． | {x∈R|-1＜x＜1} | B． | {x∈R|1≤x＜5} | C． | {x∈R|1＜x＜5} | D． | {x∈R|x≥1} |
分析 由韦恩图中阴影部分表示的集合为A∩（∁RB），然后利用集合的基本运算进行求解即可．
解答 解：A={x||x-2|＜3}={x|-1＜x＜5}，B={x|y=ln（1-x）}={x|1-x＞0}={x|x＜1}，
则∁UB={x|x≥1}，
由韦恩图中阴影部分表示的集合为A∩（∁UB），
∴A∩（∁UB）={x|1≤x＜5}，
故选：B
点评 本题主要考查集合的基本运算，利用韦恩图确定集合关系，然后利用数轴求基本运算是解决此类问题的基本方法．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
17．已知a＜0，则“ax0=b”的充要条件是（ ）
| A． | ?x∈R，$\frac{1}{2}$ax2-bx≥$\frac{1}{2}$ax02-bx0 | B． | ?x∈R，$\frac{1}{2}$ax2-bx≤$\frac{1}{2}$ax02-bx0 | ||
| C． | ?x∈R，$\frac{1}{2}$ax2-bx≤$\frac{1}{2}$ax02-bx0 | D． | ?x∈R，$\frac{1}{2}$ax2-bx≥$\frac{1}{2}$ax02-bx0 |
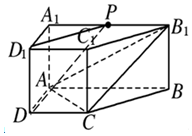直棱柱ABCD-A1B1C1D1中，底面ABCD是直角梯形，∠BAD=∠ADC=90°，AB=2AD=2CD=2．P为A1B1的中点
17．下列写法中正确的是（ ）
| A． | 0∈∅ | B． | 0∪∅={∅} | C． | 0⊆∅ | D． | ∅⊆{0} |