题目内容
10．若直线x+（1+m）y+m-2=0与直线mx+2y+6=0平行，则实数m的值是（ ）| A． | -2 | B． | 1 | C． | -2或1 | D． | m的值不存在 |
分析 利用两条直线平行，它们的斜率相等或斜率都不存在的性质求解．
解答 解：∵直线x+（1+m）y+m-2=0与直线mx+2y+6=0平行，
∴-$\frac{1}{1+m}$=-$\frac{m}{2}$，
即m2+m=2，
即（m-1）（m+2）=0
解得m=1，或m=-2，
故选：C
点评 本题考查实数值的求法，是基础题，解题时要注意直线与直线平行的性质的合理运用．
练习册系列答案
相关题目
5．若函数f（x）=$\frac{kx+7}{{k{x^2}+4kx+3}}$的定义域为R，则实数k的取值范围是（ ）
| A． | $（{0，\frac{3}{4}}）$ | B． | $（{-∞，0}）∪（{\frac{3}{4}，+∞}）$ | C． | $[{0，\frac{3}{4}}）$ | D． | $（{\frac{3}{4}，+∞}）$ |
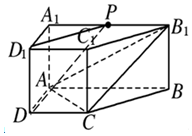直棱柱ABCD-A1B1C1D1中，底面ABCD是直角梯形，∠BAD=∠ADC=90°，AB=2AD=2CD=2．P为A1B1的中点
20．抛物线${x^2}=\frac{1}{2}y$的准线方程是（ ）
| A． | $x=\frac{1}{2}$ | B． | $x=\frac{1}{8}$ | C． | $y=\frac{1}{2}$ | D． | y=-$\frac{1}{8}$ |