题目内容
20.已知函数f(x)=x-axlnx(a≤0),$g(x)=\frac{f(x)}{x}-1$.(1)求函数f(x)单调区间;
(2)当a=-1时,
①求函数f(x)在[e-e,e]上的值域;
②求证:$\sum_{k=2}^n{\frac{1}{g(k)}}>\frac{{3{n^2}-n-2}}{n(n+1)}$,其中n∈N,n≥2.(参考数据ln2≈0.6931)
分析 (1)求出函数f(x)的导数,通过讨论a的范围求出函数的单调区间即可;
(2)将a=-1带入f(x),①求出函数的导数,根据函数的单调性求出函数的值域即可;
②设${S_n}=\frac{{3{n^2}-n-2}}{n(n+1)}$为{an}前n项和,n≥2,得到${a_n}={S_n}-{S_{n-1}}=\frac{4}{{{n^2}-1}}$,设$φ(x)=lnx-\frac{1}{4}({x^2}-1)$,根据函数的单调性证明即可.
解答 解:(1)∵f'(x)=1-alnx-a.
①当a=0时,f'(x)>0,f(x)在(0,+∞)单调递增;
②当a<0时,令1-alnx-a=0,得$lnx=\frac{1-a}{a}$,即$x={e^{\frac{1-a}{a}}}$,
∴f(x)在$(0,{e^{\frac{1-a}{a}}}]$上单调递减,在$({e^{\frac{1-a}{a}}},+∞)$单调递增.
(2)a=-1时,f(x)=x+xlnx.
①由f'(x)=2+lnx,令f'(x)=0x=e-2,
∴f(x)在[e-e,e-2]单调递减,[e-2,e]单调递增,
且由$f({e^{-e}})=\frac{1-e}{e^e}<f(e)=2e$,$f({e^{-2}})=-\frac{1}{e^2}$,
∴值域为$[{-\frac{1}{e^2},2e}]$.
证明:②由g(x)=lnx,设${S_n}=\frac{{3{n^2}-n-2}}{n(n+1)}$为{an}前n项和,n≥2,
则${a_n}={S_n}-{S_{n-1}}=\frac{4}{{{n^2}-1}}$,
设$φ(x)=lnx-\frac{1}{4}({x^2}-1)$,$φ'(x)=\frac{1}{x}-\frac{x}{2}=-\frac{{(x+\sqrt{2})(x-\sqrt{2})}}{2x}$,
φ(x)在[2,+∞)单调递减,
$φ(x)≤φ(2)=ln2-\frac{3}{4}<0$,∴$0<lnx<\frac{1}{4}({x^2}-1)$,
∴$\frac{1}{lnx}>\frac{4}{{{x^2}-1}}$,即n≥2时,$\frac{1}{lnn}>\frac{4}{{{n^2}-1}}$,
∴$\sum_{k=2}^n{\frac{1}{lnk}}$$>\sum_{m=2}^n{\frac{4}{{{m^2}-1}}}=\frac{{3{n^2}-n-2}}{n(n+1)}$,
故原不等式成立.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,考查不等式的证明,是一道综合题.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案| A. | $({-\frac{1}{2},+∞})$ | B. | $({-\frac{3}{2},+∞})$ | C. | $({-∞,-\frac{1}{2}})$ | D. | $({-∞,-\frac{3}{2}})$ |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
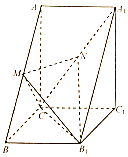 如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,∠ACB=90°,AC=CB=2,M、N分别是AB、A1C的中点.
如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,∠ACB=90°,AC=CB=2,M、N分别是AB、A1C的中点.