题目内容
在正方体ABCD-A′B′C′D′中,三棱锥A′-BC′D的体积是正方体体积的 .
考点:棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:根据要求几何体是由正方体削去4个相同的三棱锥而得,计算V正方体-4VC′-BCD可得答案.
解答:
解:设正方体ABCD-A′B′C′D′的棱长为2,
则VA′-BC′D=V正方体-4VC′-BCD=23-4×
×
×2×2×2=
,
V正方体=8,∴VA′-BC′D=
V正方体
故答案为:
.

则VA′-BC′D=V正方体-4VC′-BCD=23-4×
| 1 |
| 3 |
| 1 |
| 2 |
| 8 |
| 3 |
V正方体=8,∴VA′-BC′D=
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查了用间接法求棱锥的体积,解答的关键是根据正方体的几何特征看出要求几何体是由正方体削去4个相同的三棱锥而得.

练习册系列答案
相关题目
设复数z=
(i为虚数单位),则z的虚部为( )
| 2 |
| 1+i |
| A、-i | B、i | C、-1 | D、1 |
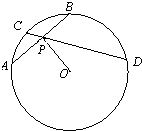 如图,⊙O的两条弦AB,CD相交于圆内一点P,若PA=PB,PC=2,PD=8,OP=4,则该圆的半径长为
如图,⊙O的两条弦AB,CD相交于圆内一点P,若PA=PB,PC=2,PD=8,OP=4,则该圆的半径长为