题目内容
4.设复数z1,z2在复平面内的对应点关于虚轴对称,z1=1+2i,i为虚数单位.则z1z2=( )| A. | 3 | B. | -5 | C. | -5i | D. | -1-4i |
分析 根据题意,写出复数z2,再计算z1z2.
解答 解:复数z1,z2在复平面内的对应点关于虚轴对称,且z1=1+2i,
∴z2=-1+2i,
∴z1z2=(1+2i)(-1+2i)=(2i)2-12=-5.
故选:B.
点评 本题考查了复数的概念与运算问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知数列{an}为等差数列,a2=2且满足a2,a3,a5成等比数列,则数列{an}的前10项的和为( )
| A. | 80 | B. | 90 | C. | 20 | D. | 20或90 |
15.设F为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)右焦点,过原点的直线与双曲线的左、右两支分别交于两点A,B,若$\overrightarrow{AF}$•$\overrightarrow{BF}$=0,且∠BAF∈($\frac{π}{12}$,$\frac{π}{6}$),则该双曲线离心率的取值范围为( )
| A. | (1,$\sqrt{2}$) | B. | (1,$\sqrt{3}$+1) | C. | ($\sqrt{2}$,+∞) | D. | ($\sqrt{2}$,$\sqrt{3}$+1) |
19.已知向量$\overrightarrow a=(x,-1)$,$\overrightarrow b=(x,4)$,其中x∈R.则“x=2”是“$\overrightarrow a⊥\overrightarrow b$”成立的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
9.已知f(x)是周期为4的奇函数,x∈[0,2]时,f(x)=$\sqrt{1-(x-1)^{2}}$.若方程f(x)-tx=0恰好有5个实根,则正实数t等于( )
| A. | $\frac{1}{5}$ | B. | $\frac{\sqrt{6}}{12}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{6}}{6}$ |
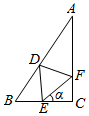 △ABC中,已知:AB=2,BC=1,CA=$\sqrt{3}$,分别在边AB,BC,CA上取点D,E,F,使△DEF是等边三角形(如图),设∠FEC=α,问当sinα=$\frac{2\sqrt{7}}{7}$时,△DEF的边长最短.
△ABC中,已知:AB=2,BC=1,CA=$\sqrt{3}$,分别在边AB,BC,CA上取点D,E,F,使△DEF是等边三角形(如图),设∠FEC=α,问当sinα=$\frac{2\sqrt{7}}{7}$时,△DEF的边长最短.