题目内容
9.已知f(x)是周期为4的奇函数,x∈[0,2]时,f(x)=$\sqrt{1-(x-1)^{2}}$.若方程f(x)-tx=0恰好有5个实根,则正实数t等于( )| A. | $\frac{1}{5}$ | B. | $\frac{\sqrt{6}}{12}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{6}}{6}$ |
分析 根据函数奇偶性和周期性的关系求出函数的解析式,利用函数与方程的关系转化为两个函数的交点个数问题,利用数形结合进行求解即可.
解答 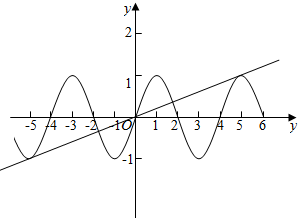 解:若x∈[-2,0],则-x∈[0,2],
解:若x∈[-2,0],则-x∈[0,2],
则f(-x)=$\sqrt{1-(-x-1)^{2}}$,
∵f(x)是周期为4的奇函数,
∴f(-x)=$\sqrt{1-(-x-1)^{2}}$=-f(x)
即f(x)=-$\sqrt{1-(x+1)^{2}}$,x∈[-2,0],
由f(x)-tx=0得f(x)=tx,
作出函数f(x)与g(x)=tx的图象如图:
要使方程f(x)-tx=0恰好有5个实根,
则只需要当x>0时f(x)与g(x)有两个交点,
即当x∈[4,6]时,g(x)与f(x)相切,即可.
当当x∈[4,6]时,当x-4∈[0,2],
则f(x)=f(x-4)=$\sqrt{1-(x-4-1)^{2}}$=$\sqrt{1-(x-5)^{2}}$,此时圆心为(5,0),半径R=1,
则圆心到直线tx-y=0的距离d=$\frac{5t}{\sqrt{{t}^{2}+1}}$=1,
得t=$\frac{\sqrt{6}}{12}$,
故选:B.
点评 本题主要考查函数与方程的应用,利用函数奇偶性和周期性的关系求出函数的解析式,转化为两个函数的交点问题是解决本题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
19.设复数z满足(z-1)(1+i)=2(i为虚数单位),则|z|=( )
| A. | 1 | B. | 5 | C. | $\sqrt{5}$ | D. | $\sqrt{13}$ |
4.设复数z1,z2在复平面内的对应点关于虚轴对称,z1=1+2i,i为虚数单位.则z1z2=( )
| A. | 3 | B. | -5 | C. | -5i | D. | -1-4i |
1.已知点F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,点E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A,B两点,若△ABE是钝角三角形,则该双曲线的离心率的取值范围是( )
| A. | (1,$\sqrt{2}$) | B. | ($\sqrt{2}$,+∞) | C. | (1,2) | D. | (2,+∞) |
18.已知tanα=1,那么$\frac{sinα-2cosα}{3sinα+cosα}$=( )
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -4 | D. | 4 |