题目内容
14.已知数列{an}为等差数列,a2=2且满足a2,a3,a5成等比数列,则数列{an}的前10项的和为( )| A. | 80 | B. | 90 | C. | 20 | D. | 20或90 |
分析 先根据等比中项的性质求出公差d,再根据等差数列的前n项和公式计算即可.
解答 解:a2,a3,a5成等比数,
∴(a2+d)2=a2•(a2+3d),
∴(2+d)2=2•(2+3d),
解得d=0或d=2,
∴a1=2,或a1=0,
当d=0时,S10=10a1=20,
当d=2,S10=10a1+$\frac{10(10-1)×2}{2}$=90,
故选:D.
点评 本题考查了等差数列的通项公式和前n项和公式,属于基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
4.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线方程为y=±$\frac{\sqrt{2}}{2}$x,则此双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{3}{2}$ |
2. 某人在连续7天的定点投篮的分数统计如下:在上述统计数据的分析中,一部分计算如右图所示的算法流程图(其中$\overline{a}$是这7个数据的平均数),则输出的S的值是( )
某人在连续7天的定点投篮的分数统计如下:在上述统计数据的分析中,一部分计算如右图所示的算法流程图(其中$\overline{a}$是这7个数据的平均数),则输出的S的值是( )
 某人在连续7天的定点投篮的分数统计如下:在上述统计数据的分析中,一部分计算如右图所示的算法流程图(其中$\overline{a}$是这7个数据的平均数),则输出的S的值是( )
某人在连续7天的定点投篮的分数统计如下:在上述统计数据的分析中,一部分计算如右图所示的算法流程图(其中$\overline{a}$是这7个数据的平均数),则输出的S的值是( )| 观测次数i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 观测数据ai | 5 | 6 | 8 | 6 | 8 | 8 | 8 |
| A. | 1 | B. | $\frac{8}{7}$ | C. | $\frac{9}{7}$ | D. | $\frac{10}{7}$ |
19.设复数z满足(z-1)(1+i)=2(i为虚数单位),则|z|=( )
| A. | 1 | B. | 5 | C. | $\sqrt{5}$ | D. | $\sqrt{13}$ |
3.设直线l与平面α平行,直线m在平面α上,那么( )
| A. | 直线l平行于直线m | B. | 直线l与直线m异面 | ||
| C. | 直线l与直线m没有公共点 | D. | 直线l与直线m不垂直 |
4.设复数z1,z2在复平面内的对应点关于虚轴对称,z1=1+2i,i为虚数单位.则z1z2=( )
| A. | 3 | B. | -5 | C. | -5i | D. | -1-4i |
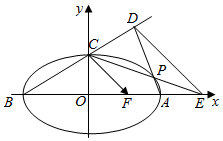 如图:A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的顶点,点F(c,0)为椭圆的右焦点,原点O到直线CF的距离为$\frac{1}{2}c$,且椭圆过点$({2\sqrt{3},1})$.
如图:A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的顶点,点F(c,0)为椭圆的右焦点,原点O到直线CF的距离为$\frac{1}{2}c$,且椭圆过点$({2\sqrt{3},1})$.