题目内容
12.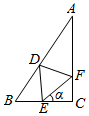 △ABC中,已知:AB=2,BC=1,CA=$\sqrt{3}$,分别在边AB,BC,CA上取点D,E,F,使△DEF是等边三角形(如图),设∠FEC=α,问当sinα=$\frac{2\sqrt{7}}{7}$时,△DEF的边长最短.
△ABC中,已知:AB=2,BC=1,CA=$\sqrt{3}$,分别在边AB,BC,CA上取点D,E,F,使△DEF是等边三角形(如图),设∠FEC=α,问当sinα=$\frac{2\sqrt{7}}{7}$时,△DEF的边长最短.
分析 设等边△DEF的边长为x,显然∠C=90°,∠B=60°,EC=x•cosα,得到∠EDB=α,在三角形BDE中,利用正弦定理列出关系式,表示出BE,由BE+EC=BC,列出关于x的方程,求出方程的解得到x的值,得到三角形的边长,求出边长的最小值,以及此时sinα的值即可.
解答 解:设等边△DEF的边长为x,显然∠C=90°,∠B=60°,EC=x•cosα,
∵∠DEC=∠DEF+α=∠EDB+∠B,∴∠EDB=α.
在△BDE中,由正弦定理得$\frac{x}{sin60°}$=$\frac{BE}{sinα}$,∴BE=$\frac{2\sqrt{3}}{3}•x•sinα$xsinα,
∵BE+EC=BC,∴xcosα+$\frac{2\sqrt{3}}{3}•x•sinα$=1,
∴x=$\frac{1}{cosα+\frac{2\sqrt{3}}{3}•sinα}$=$\frac{\sqrt{3}}{\sqrt{7}•(\sqrt{\frac{3}{7}}•cosα+\frac{2}{\sqrt{7}}sinα)}$=$\frac{\sqrt{3}}{\sqrt{7}•sin(α+θ)}$,
(其中,cosθ=$\frac{2}{\sqrt{7}}$,sinθ=$\sqrt{\frac{3}{7}}$),
当α+θ=$\frac{π}{2}$,即α=$\frac{π}{2}$-θ时,xmin=$\frac{\sqrt{21}}{7}$,此时sinα=cosθ=$\frac{2\sqrt{7}}{7}$,
故答案为:$\frac{{2\sqrt{7}}}{7}$.
点评 此题考查了正弦定理,正弦函数的值域,以及两角和与差的正弦函数公式,熟练掌握正弦定理是解本题的关键,属于中档题.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案 某人在连续7天的定点投篮的分数统计如下:在上述统计数据的分析中,一部分计算如右图所示的算法流程图(其中$\overline{a}$是这7个数据的平均数),则输出的S的值是( )
某人在连续7天的定点投篮的分数统计如下:在上述统计数据的分析中,一部分计算如右图所示的算法流程图(其中$\overline{a}$是这7个数据的平均数),则输出的S的值是( )| 观测次数i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 观测数据ai | 5 | 6 | 8 | 6 | 8 | 8 | 8 |
| A. | 1 | B. | $\frac{8}{7}$ | C. | $\frac{9}{7}$ | D. | $\frac{10}{7}$ |
| A. | 直线l平行于直线m | B. | 直线l与直线m异面 | ||
| C. | 直线l与直线m没有公共点 | D. | 直线l与直线m不垂直 |
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
| A. | 3 | B. | -5 | C. | -5i | D. | -1-4i |
| A. | (1,$\sqrt{2}$) | B. | ($\sqrt{2}$,+∞) | C. | (1,2) | D. | (2,+∞) |