题目内容
若
,
是两个非零向量,且|
|=|
|=λ|
+
|,λ∈[
,1],则
与
-
的夹角的取值范围是( )
| a |
| b |
| a |
| b |
| a |
| b |
| ||
| 3 |
| b |
| a |
| b |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
考点:平面向量数量积的运算
专题:计算题,不等式的解法及应用,平面向量及应用
分析:不妨设|
+
|=1,则|
|=|
|=λ,运用向量的平方即为模的平方,可得
•
=
,再由向量的夹角公式,求得cos<
,
-
>=-
,再由λ∈[
,1],运用不等式的性质,结合余弦函数的单调性,即可得到所求范围.
| a |
| b |
| a |
| b |
| a |
| b |
| 1-2λ2 |
| 2 |
| b |
| a |
| b |
1-
|
| ||
| 3 |
解答:
解:由于|
|=|
|=λ|
+
|,λ∈[
,1],
不妨设|
+
|=1,则|
|=|
|=λ,
即有(
+
)2=
2+
2+2
•
=2λ2+2
•
=1,
即
•
=
,
•(
-
)=
•
-
2=
-λ2=
,
|
-
|=
=
=
=
,
cos<
,
-
>=
=-
=-
=-
,
由于λ∈[
,1],则λ2∈[
,1],
∈[
,
],
-
∈[-
,-
],
由于0≤<
,
-
>≤π,
则有
≤<
,
-
>≤
.
故选B.
| a |
| b |
| a |
| b |
| ||
| 3 |
不妨设|
| a |
| b |
| a |
| b |
即有(
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
即
| a |
| b |
| 1-2λ2 |
| 2 |
| b |
| a |
| b |
| a |
| b |
| b |
| 1-2λ2 |
| 2 |
| 1-4λ2 |
| 2 |
|
| a |
| b |
(
|
|
| 2λ2-(1-2λ2) |
| 4λ2-1 |
cos<
| b |
| a |
| b |
| ||||||
|
|
| 1-4λ2 | ||
2λ
|
| ||
| 2λ |
1-
|
由于λ∈[
| ||
| 3 |
| 1 |
| 3 |
| 1 |
| 4λ2 |
| 1 |
| 4 |
| 3 |
| 4 |
-
1-
|
| ||
| 2 |
| 1 |
| 2 |
由于0≤<
| b |
| a |
| b |
则有
| 2π |
| 3 |
| b |
| a |
| b |
| 5π |
| 6 |
故选B.
点评:本题主要考查向量的数量积的性质:向量的平方即为模的平方,考查向量的夹角的范围,运用不等式的性质是解题的关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
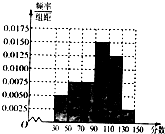 从某校高一期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图,如图所示.根据频率分布直方图,估计该次数学考试的平均分为( )
从某校高一期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图,如图所示.根据频率分布直方图,估计该次数学考试的平均分为( )| A、46 | B、82 | C、92 | D、102 |
如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )


A、(2+
| ||
| B、4π | ||
C、(2+2
| ||
| D、6π |
 如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,侧面是正方形,∠DAB=60°,E是棱CB的延长线上一点,经过点A、C1、E的平面交棱BB1于点F,B1F=2BF.
如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,侧面是正方形,∠DAB=60°,E是棱CB的延长线上一点,经过点A、C1、E的平面交棱BB1于点F,B1F=2BF. 图①是边长为30cm的正方形纸板,裁掉阴影部分后将其折叠成图②所示的长方体盒子,已知该长方体的宽是高的2倍,则它的体积是
图①是边长为30cm的正方形纸板,裁掉阴影部分后将其折叠成图②所示的长方体盒子,已知该长方体的宽是高的2倍,则它的体积是 为了调查某校学生体质健康达标情况,现采用随机抽样的方法从该校抽取了m名学生进行体育测试.根据体育测试得到了这m名学生各项平均成绩(满分100分),按照以下区间分为七组:[30,40),[40,50),[50,60),[60,70),[70,80),[80,90),[90,100),并得到频率分布直方图(如图),己知测试平均成绩在区间[30,60)有20人.
为了调查某校学生体质健康达标情况,现采用随机抽样的方法从该校抽取了m名学生进行体育测试.根据体育测试得到了这m名学生各项平均成绩(满分100分),按照以下区间分为七组:[30,40),[40,50),[50,60),[60,70),[70,80),[80,90),[90,100),并得到频率分布直方图(如图),己知测试平均成绩在区间[30,60)有20人.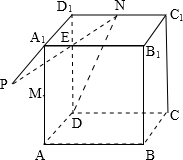 如图,在一封闭的正方体容器内装满水,M、N分别是AA1与C1D1的中点,由于某种原因,在D、M、N三点处各有一个小洞,为此容器内存水最多,问应将此容器如何放置?此时水的上表面的形状怎样?
如图,在一封闭的正方体容器内装满水,M、N分别是AA1与C1D1的中点,由于某种原因,在D、M、N三点处各有一个小洞,为此容器内存水最多,问应将此容器如何放置?此时水的上表面的形状怎样?