题目内容
若双曲线C:
-
=1的一条渐近线的倾斜角为
,则双曲线C的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 6 |
A、2或
| ||||
B、
| ||||
C、2或
| ||||
| D、2 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:求出双曲线的渐近线方程,可得b=
a,再由a,b,c的关系和离心率公式,即可得到双曲线的离心率.
| ||
| 3 |
解答:
解:双曲线C:
-
=1的渐近线方程为y=±
x,
则tan
=
即为b=
a,则c=
=
a,
即有e=
=
.
故选:B.
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
则tan
| π |
| 6 |
| b |
| a |
| ||
| 3 |
| a2+b2 |
2
| ||
| 3 |
即有e=
| c |
| a |
2
| ||
| 3 |
故选:B.
点评:本题考查双曲线的方程和性质,考查离心率的求法,考查运算能力,属于基础题.

练习册系列答案
相关题目
如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )


A、(2+
| ||
| B、4π | ||
C、(2+2
| ||
| D、6π |
某单位为了了解办公楼用电量y(度)与气温x(℃)之间的关系,随机统计了四个工作量与当天平均气温,并制作了对照表:
由表中数据得到线性回归方程
=-2x+a,当气温为-4℃时,预测用电量均为( )
| 气温(℃) | 18 | 13 | 10 | -1 |
| 用电量(度) | 24 | 34 | 38 | 64 |
 |
| y |
| A、68度 | B、52度 |
| C、12度 | D、28度 |
函数f(x)=xcosx2在区间[0,3]上的零点的个数为( )
| A、2 | B、3 | C、4 | D、5 |
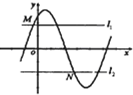 如图:M(xM,yM),N(xN,yN)分别是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象与两条直线l1:y=m,l2:y=-m(A≥m≥0)的两个交点,记S=|xN-xM|,则S(m)图象大致是( )
如图:M(xM,yM),N(xN,yN)分别是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象与两条直线l1:y=m,l2:y=-m(A≥m≥0)的两个交点,记S=|xN-xM|,则S(m)图象大致是( )


