题目内容
已知
,
,
是单位向量,
⊥
,则(
+
+2
)•
的最大值是 .
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
| c |
考点:平面向量数量积的运算
专题:平面向量及应用
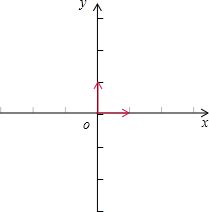
分析:建系,可得
=(1,0),
=(0,1),并设
=(cosθ,sinθ),可得
+
+2
的坐标,由数量积的运算可得(
+
+2
)•
的表达式,由三角函数的知识可得.
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| c |
解答:
解:由题意,分别以向量
,
作为x、y轴的单位向量建立直角坐标系,
则可得
=(1,0),
=(0,1),并设
=(cosθ,sinθ),
则可得
+
+2
=(1+2cosθ,1+2sinθ),
∴(
+
+2
)•
=(1+2cosθ)cosθ+(1+2sinθ)sinθ
=cosθ+2cos2θ+sinθ+2sin2θ=cosθ+sinθ+2
=
sin(θ+
)+2,
由三角函数的知识可知,当θ=
时,上式取最大值
+2
故答案为:
+2
| a |
| b |
则可得
| a |
| b |
| c |
则可得
| a |
| b |
| c |
∴(
| a |
| b |
| c |
| c |
=cosθ+2cos2θ+sinθ+2sin2θ=cosθ+sinθ+2
=
| 2 |
| π |
| 4 |
由三角函数的知识可知,当θ=
| π |
| 4 |
| 2 |
故答案为:
| 2 |

点评:本题考查平面向量数量积的运算,涉及三角函数的应用,属中档题.

练习册系列答案
相关题目
化简代数式
+
的结果是( )
3+2
|
3-2
|
| A、3 | ||
B、1+
| ||
C、2+
| ||
D、2
|
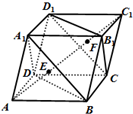 已知平行六面体ABCD-A1B1C1D1,AC1与平面A1BD,CB1D1交于E,F两点.给出以下命题,其中真命题有
已知平行六面体ABCD-A1B1C1D1,AC1与平面A1BD,CB1D1交于E,F两点.给出以下命题,其中真命题有