题目内容
已知动点P到定点F(1,0)的距离比到直线x+2=0的距离小1.
(1)求动点P的轨迹E的方程;
(2)若曲线E上存在A、B两点关于直线l:2x+4y-9=0对称,且线段AB的延长线与直线x+1=0相交于点C,求:
(i)直线AB的方程;
(ii)△FAB与△FCB的面积之比.
(1)求动点P的轨迹E的方程;
(2)若曲线E上存在A、B两点关于直线l:2x+4y-9=0对称,且线段AB的延长线与直线x+1=0相交于点C,求:
(i)直线AB的方程;
(ii)△FAB与△FCB的面积之比.
考点:直线与圆锥曲线的综合问题,轨迹方程
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意可得动点P到定点F(1,0)的距离与到直线x+1=0的距离相等.可得动点P的轨迹E是抛物线.
(2)(i)设A(x1,y1),B(x2,y2),线段AB的中点M(x0,y0),把A,B的坐标代入抛物线方程可得:
=4x1,
=4y2,相减可得2y0•kAB=4,由直线l的斜率kl=-
,可得kAB=2,解得y0,代入直线l的方程可得M,利用点斜式可得直线AB的方程.
(ii)令x=-1,代入直线AB的方程解得C.联立
,解得A,B,利用
=
即可得出.
(2)(i)设A(x1,y1),B(x2,y2),线段AB的中点M(x0,y0),把A,B的坐标代入抛物线方程可得:
| y | 2 1 |
| y | 2 2 |
| 1 |
| 2 |
(ii)令x=-1,代入直线AB的方程解得C.联立
|
| S△FAB |
| S△FBC |
| |AB| |
| |BC| |
解答:
解:(1)由题意可得动点P到定点F(1,0)的距离与到直线x+1=0的距离相等.
∴动点P的轨迹E是抛物线:点F为焦点,直线x=-1为准线,可得方程为:y2=4x.
(2)(i)设A(x1,y1),B(x2,y2),线段AB的中点M(x0,y0),
把A,B的坐标代入抛物线方程可得:
=4x1,
=4y2,
相减可得
=4,
∴2y0•kAB=4,
∵kAB×(-
)=-1,
∴kAB=2.∴2y0=2,解得y0=1,
代入方程2x+4y-9=0可得2x0+4-9=0,解得x0=
.
∴M(
,1),可得直线AB的方程为:y-1=2(x-
),化为2x-y-4=0.
(ii)令x=-1,代入直线AB的方程2x-y-4=0,解得y=-6,∴C(-1,-6).
联立
,解得
或
,
∴A(4,4),B(1,-2),|AB|=
=3
,|BC|=
=2
.
∴
=
=
.
∴动点P的轨迹E是抛物线:点F为焦点,直线x=-1为准线,可得方程为:y2=4x.
(2)(i)设A(x1,y1),B(x2,y2),线段AB的中点M(x0,y0),
把A,B的坐标代入抛物线方程可得:
| y | 2 1 |
| y | 2 2 |
相减可得
| (y1-y2)(y1+y2) |
| x1-x2 |
∴2y0•kAB=4,
∵kAB×(-
| 1 |
| 2 |
∴kAB=2.∴2y0=2,解得y0=1,
代入方程2x+4y-9=0可得2x0+4-9=0,解得x0=
| 5 |
| 2 |
∴M(
| 5 |
| 2 |
| 5 |
| 2 |
(ii)令x=-1,代入直线AB的方程2x-y-4=0,解得y=-6,∴C(-1,-6).
联立
|
|
|
∴A(4,4),B(1,-2),|AB|=
| 32+62 |
| 5 |
| 22+42 |
| 5 |
∴
| S△FAB |
| S△FBC |
| |AB| |
| |BC| |
| 3 |
| 2 |
点评:本题考查了抛物线的标准方程及其性质、直线与抛物线相交问题转化为方程联立得出交点、两点之间的距离公式、三角形面积之比、线段的垂直平分线的性质、中点坐标公式,考查了推理能力与计算能力,属于难题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 如图,抛物线y=ax2-
如图,抛物线y=ax2-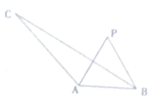 如图所示,在△ABC中,∠BAC=120°,AC=3,AB=1,P为∠BAC平分线上异于A的一点,∠APB=α,三角形PAB的面积记为S.
如图所示,在△ABC中,∠BAC=120°,AC=3,AB=1,P为∠BAC平分线上异于A的一点,∠APB=α,三角形PAB的面积记为S. 经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其他鱼偏高.《中华人民共和国环境保护法》规定食品的汞含量不得超过1.0ppm,现从一批数量很大的罗非鱼中随机地抽出15条作为样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后第一位数字为叶)如图所示
经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其他鱼偏高.《中华人民共和国环境保护法》规定食品的汞含量不得超过1.0ppm,现从一批数量很大的罗非鱼中随机地抽出15条作为样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后第一位数字为叶)如图所示