题目内容
直线l与直线l1:x-3y+10=0和直线l2:2x+y-8=0分别交于M,N两点,且MN的中点坐标为(0,1),则直线l的方程为( )
| A、x+4y-4=0 |
| B、4x+y-4=0 |
| C、x-4y+4=0 |
| D、x-4y-4=0 |
考点:两条直线的交点坐标
专题:直线与圆
分析:利用中点坐标公式及中心对称即可得出点M的坐标,再利用点斜式即可得出.
解答:
解:设M(m,n),N(s,t),
∵MN的中点坐标为P(0,1),∴
,解得
.
又点M,N分别在直线l1,l2上,∴
,解得
.
∴M(-4,2).
∴kl=kMP=
=-
,
∴直线l的方程为y=-
x+1,化为x+4y-4=0.
故选A.
∵MN的中点坐标为P(0,1),∴
|
|
又点M,N分别在直线l1,l2上,∴
|
|
∴M(-4,2).
∴kl=kMP=
| 2-1 |
| -4-0 |
| 1 |
| 4 |
∴直线l的方程为y=-
| 1 |
| 4 |
故选A.
点评:本题考查了中点坐标公式及中心对称、点斜式等基础知识,属于基础题.

练习册系列答案
相关题目
若f(x)=1-
,则f(2)等于( )
| 1 |
| x2 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
已知圆C的方程为(x-2)2+(y-1)2=25,A(3,4)为定点,过A的两条弦MN、PQ互相垂直,记四边形MPNQ面积的最大值与最小值分别为S1,S2,则
-
是( )
| S | 2 1 |
| S | 2 2 |
| A、200 | B、100 |
| C、64 | D、36 |
如图是一几何体的三视图,则此几何体的体积是( )
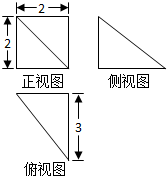

| A、4 | B、8 | C、12 | D、4π |
如果直线x+2y-1=0和kx-y-3=0互相平行,则实数k的值为( )
A、-
| ||
| B、-2 | ||
| C、2 | ||
D、
|