题目内容
已知数列{an}中,a1=t(t为非零常数),其前n项和为Sn,满足an+1=2Sn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若对任意的n∈N*,都有λan>n(n+1)成立,求实数λ的取值范围.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若对任意的n∈N*,都有λan>n(n+1)成立,求实数λ的取值范围.
考点:数列与不等式的综合,数列递推式
专题:点列、递归数列与数学归纳法,不等式的解法及应用
分析:(Ⅰ)由数列递推式求出a2,再由an=Sn-Sn-1(n≥2)整理得到
=3 (n≥2),由等比数列的通项公式求出n≥2时的通项,验证n=1时不成立,则数列{an}的通项公式可求;
(Ⅱ)把an代入λan>n(n+1),利用数学转化思想方法把不等式恒等变形,分离参数λ,然后对t分类,利用数列的函数特性求得t在不同范围内的最值,则实数λ的取值范围可求.
| an+1 |
| an |
(Ⅱ)把an代入λan>n(n+1),利用数学转化思想方法把不等式恒等变形,分离参数λ,然后对t分类,利用数列的函数特性求得t在不同范围内的最值,则实数λ的取值范围可求.
解答:
解:(Ⅰ)当n=1时,a1=t,
当n≥2时,an=Sn-Sn-1=
an+1-
an,
即an+1=3an (n≥2),
又a1=t≠0,
∴
=3 (n≥2),
又a2=2S1=2t,
∴当n≥2时,数列{an}是以a2为首项,3为公比的等比数列.
∴an=2t•3n-2 (n≥2),
又∵a1=t不适合上式,
∴an=
;
(Ⅱ)当t>0时,λan>n(n+1)成立,等价于λ大于
的最大值.
当n=1时,有λ>
,
当n≥2时,令bn=
,
bn+1-bn=
-
=
(n+2-3n)=
<0.
∴当n≥2时,数列{an}为递减数列,
∴当n≥2时,bn≤b2=
.
∴当t>0时,λ>
.
当t<0时,λan>n(n+1)成立,等价于λ大于
的最小值.
当n=1时,有λ<
,
当n≥2时,令bn=
,
bn+1-bn=
-
=
(n+2-3n)=
>0.
∴当n≥2时,数列{bn}为递增数列,
∴当n≥2时,bn≥b2=
.
∴当t<0时,λ<
.
综上所述,当t>0时,λ>
;
当t<0时,λ<
.
当n≥2时,an=Sn-Sn-1=
| 1 |
| 2 |
| 1 |
| 2 |
即an+1=3an (n≥2),
又a1=t≠0,
∴
| an+1 |
| an |
又a2=2S1=2t,
∴当n≥2时,数列{an}是以a2为首项,3为公比的等比数列.
∴an=2t•3n-2 (n≥2),
又∵a1=t不适合上式,
∴an=
|
(Ⅱ)当t>0时,λan>n(n+1)成立,等价于λ大于
| n(n+1) |
| an |
当n=1时,有λ>
| 2 |
| t |
当n≥2时,令bn=
| n(n+1) |
| 2t•3n-2 |
bn+1-bn=
| (n+1)(n+2) |
| 2t•3n-1 |
| n(n+1) |
| 2t•3n-2 |
=
| n+1 |
| 2t•3n-1 |
| 1-n2 |
| t•3n-1 |
∴当n≥2时,数列{an}为递减数列,
∴当n≥2时,bn≤b2=
| 3 |
| t |
∴当t>0时,λ>
| 3 |
| t |
当t<0时,λan>n(n+1)成立,等价于λ大于
| n(n+1) |
| an |
当n=1时,有λ<
| 2 |
| t |
当n≥2时,令bn=
| n(n+1) |
| 2t•3n-2 |
bn+1-bn=
| (n+1)(n+2) |
| 2t•3n-1 |
| n(n+1) |
| 2t•3n-2 |
=
| n+1 |
| 2t•3n-1 |
| 1-n2 |
| t•3n-1 |
∴当n≥2时,数列{bn}为递增数列,
∴当n≥2时,bn≥b2=
| 3 |
| t |
∴当t<0时,λ<
| 3 |
| t |
综上所述,当t>0时,λ>
| 3 |
| t |
当t<0时,λ<
| 3 |
| t |
点评:本题是数列与不等式的综合题,考查了由数列递推式求数列的通项公式,考查了与数列有关的恒成立问题,体现了分类讨论的数学思想方法,是中高档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知实数x∈[1,10],执行如图所示的程序框图,则输出x的值不小于55的概率为( )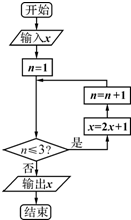

A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,向量
如图,向量| OZ |
| 4 |
| z |
| A、1+3i | B、-3+i |
| C、3-i | D、3+i |