题目内容
在△ABC中,角A、B、C所对的边分别为a、b、c,且BC边上的高为
a,则
+
的最大值是( )
| ||
| 6 |
| c |
| b |
| b |
| c |
| A、8 | ||
| B、6 | ||
C、3
| ||
| D、4 |
考点:基本不等式在最值问题中的应用
专题:综合题,解三角形
分析:利用三角形的面积公式、余弦定理,化简
+
,再利用辅助角公式,即可求得结论.
| c |
| b |
| b |
| c |
解答:
解:
+
=
,这个形式很容易联想到余弦定理:cosA=
①
而条件中的“高”容易联想到面积,a•
a=bcsinA,
即a2=2
bcsinA②,将②代入①得:
b2+c2=2bc(cosA+
sinA),
∴
+
=2(cosA+
sinA)=4sin(A+
),当A=
时取得最大值4,
故选D.
| c |
| b |
| b |
| c |
| c2+b2 |
| bc |
| b2+c2-a2 |
| 2bc |
而条件中的“高”容易联想到面积,a•
| ||
| 6 |
即a2=2
| 3 |
b2+c2=2bc(cosA+
| 3 |
∴
| c |
| b |
| b |
| c |
| 3 |
| π |
| 6 |
| π |
| 3 |
故选D.
点评:本题考查余弦定理及其应用,考查辅助角公式,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
不等式log3|x-
|<-1的解集是( )
| 1 |
| 3 |
A、(0,
| ||||||
B、(
| ||||||
C、(0,
| ||||||
D、(
|
命题“?x>1,使x2-2x-3≤0”的否定形式为( )
| A、?x≤1使x2-2x-3>0 |
| B、?x>1均有x2-2x-3>0 |
| C、?x≤1均有x2-2x-3>0 |
| D、?x≤1使x2-2x-3>0 |
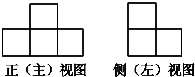 用小正方体搭成一个几何体,如图是它的正(主)视图和侧(左)视图,搭成这个几何体的小正方体最多为
用小正方体搭成一个几何体,如图是它的正(主)视图和侧(左)视图,搭成这个几何体的小正方体最多为