题目内容
11.若直线l1:x-2y+1=0与l2:2x+ay-2=0平行,则l1与l2的距离为( )| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{2\sqrt{5}}}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{2}{5}$ |
分析 根据直线平行求出a的值,根据平行线间的距离公式计算即可.
解答 解:若直线l1:x-2y+1=0与l2:2x+ay-2=0平行,
则$\frac{1}{2}$=$\frac{-2}{a}$≠$\frac{1}{-2}$,解得:a=-4,
故l1:x-2y+1=0与l2:x-2y-1=0的距离是:
d=$\frac{2}{\sqrt{1+4}}$=$\frac{2\sqrt{5}}{5}$,
故选:B.
点评 本题考查了直线的位置关系,考查平行线间的距离公式,是一道基础题.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
19.已知命题p:f(x)=lnx+2x2+6mx+1在(0,+∞)上单调递增,q:m≥-5,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
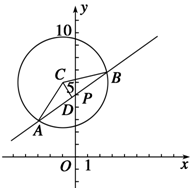 已知圆C过P(2,6),Q(-2,2)两点,且圆心C在直线3x+y=0上.
已知圆C过P(2,6),Q(-2,2)两点,且圆心C在直线3x+y=0上.