题目内容
已知全集U=R,A={x|x≥3},B={x|x2-8x+7≤0},C={x|x≥a}.则A∩B= ;若C∪A=A,则实数a的取值范围是 .
考点:交集及其运算,并集及其运算
专题:集合
分析:利用交集和并集的性质求解.
解答:
解:∵全集U=R,A={x|x≥3},B={x|x2-8x+7≤0}={x|1≤x≤7},
∴A∩B={x|3≤x≤7}=[3,7].
∵C={x|x≥a},C∪A=A,
∴C⊆A,∴a≥3,即实数a的取值范围是[3,+∞).
故答案为:[3,7];[3,+∞).
∴A∩B={x|3≤x≤7}=[3,7].
∵C={x|x≥a},C∪A=A,
∴C⊆A,∴a≥3,即实数a的取值范围是[3,+∞).
故答案为:[3,7];[3,+∞).
点评:本题考查并集和交集的求法和应用,是基础题,解题时要注意不等式的性质的合理运用.

练习册系列答案
相关题目
已知x、y满足条件
,则4x+2y的最小值为( )
|
| A、5 | B、-5 | C、12 | D、-12 |
若直线y=2ax-2与y=(a+2)x+1平行,则a=( )
| A、2 | B、1 | C、-1 | D、0 |
 如图,正方体ABCD-A1B1C1D1中,AB=2,则三棱锥A-A1B1C的体积是
如图,正方体ABCD-A1B1C1D1中,AB=2,则三棱锥A-A1B1C的体积是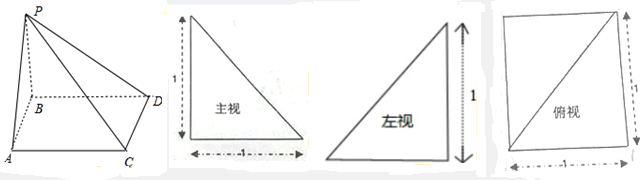 (1)求四棱锥的体积和表面积;
(1)求四棱锥的体积和表面积;