题目内容
已知sin2a=
，则
-
的值为 ．
| 1 |
| 3 |
| 1 |
| tana |
| 1 |
| tan2a |
考点：三角函数的化简求值
专题：三角函数的求值
分析：把要求解的代数式化切为弦，转化为含有sin2a的代数式得答案．
解答：
解：∵sin2a=
，
∴
-
=
-
=
-
=
=
=
=3．
| 1 |
| 3 |
∴
| 1 |
| tana |
| 1 |
| tan2a |
| 1 | ||
|
| 1 | ||
|
=
| cosa |
| sina |
| cos2a |
| sin2a |
| 2cos2a-cos2a |
| sin2a |
=
| 1 |
| sin2a |
| 1 | ||
|
点评：本题考查了三角函数的化简与求值，考查了同角三角函数的基本关系式，是基础题．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
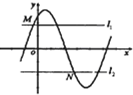如图：M（xM，yM），N（xN，yN）分别是函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）的图象与两条直线l1：y=m，l2：y=-m（A≥m≥0）的两个交点，记S=|xN-xM|，则S（m）图象大致是（ ）
在△ABC中，角A，B，C所对的边分别为a，b，c，c=1，B=45°，cosA=
，则b等于（ ）
| 3 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
