题目内容
18.在等比数列{an}中,已知a4=27a3,则$\frac{{a}_{2}}{{a}_{1}}$+$\frac{{a}_{4}}{{a}_{2}}$+$\frac{{a}_{6}}{{a}_{3}}$+…+$\frac{{a}_{2n}}{{a}_{n}}$等于( )| A. | $\frac{{3}^{-n}-3}{2}$ | B. | $\frac{{3}^{1-n}-3}{2}$ | C. | $\frac{{3}^{n}-3}{2}$ | D. | $\frac{{3}^{n+1}-3}{2}$ |
分析 由已知求得等比数列的公比,然后再由等比数列的前n项和公式求得答案.
解答 解:在等比数列{an}中,由a6=27a3,得q=3,
∴$\frac{{a}_{2}}{{a}_{1}}$+$\frac{{a}_{4}}{{a}_{2}}$+$\frac{{a}_{6}}{{a}_{3}}$+…+$\frac{{a}_{2n}}{{a}_{n}}$=q+q2+q3+…+qn=$\frac{q(1-{q}^{n})}{1-q}=\frac{3(1-{3}^{n})}{1-3}=\frac{{3}^{n+1}-3}{2}$.
故选:D.
点评 本题考查等比数列的通项公式,考查了等比数列的性质,是基础的计算题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.将函数f(x)=sin(2x-$\frac{π}{3}$)的图象向左平移φ(φ>0)个单位,所得图象对应的函数为奇函数,则φ的最小值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
8.数学活动小组由12名同学组成,现将这12名同学平均分成四组分别研究四个不同课题,且每组只研究一个课题,并要求每组选出一名组长,则不同的分配方案有( )种.
| A. | $\frac{{C}_{12}^{3}{C}_{9}^{3}{C}_{6}^{3}}{{A}_{3}^{3}}$A${\;}_{4}^{4}$ | B. | C${\;}_{12}^{3}$C${\;}_{9}^{3}$C${\;}_{6}^{3}$34 | ||
| C. | $\frac{{C}_{12}^{3}{C}_{9}^{3}{C}_{6}^{3}}{{A}_{4}^{4}}$43 | D. | C${\;}_{12}^{3}$C${\;}_{9}^{3}$C${\;}_{6}^{3}$43 |
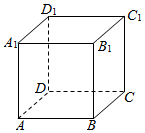 如图,正方体ABCD-A1B1C1D1的棱长为1,请在此正方体中取出四个顶点构成一个三棱锥,满足三棱锥的四个面都是直角三角形,并求此三棱锥的体积.
如图,正方体ABCD-A1B1C1D1的棱长为1,请在此正方体中取出四个顶点构成一个三棱锥,满足三棱锥的四个面都是直角三角形,并求此三棱锥的体积.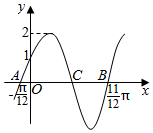
 在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图:
在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图: