题目内容
 在梯形ABCD中,AB∥CD,如果分别以下列各选项所给的内容作为已知条件,那么其中不能确定BD长度的选项是( )
在梯形ABCD中,AB∥CD,如果分别以下列各选项所给的内容作为已知条件,那么其中不能确定BD长度的选项是( )| A、AC=4,∠ABD=45°,∠ACD=30° | ||
B、AB=2,CD=2
| ||
C、AB=2,CD=2
| ||
D、CD=2
|
考点:解三角形
专题:解三角形
分析:首先判断出B,C中的条件能够确定梯形ABCD,则BD长度能确定,然后由A的条件可得梯形BD长度能确定,则答案可求.
解答:
解:对于A,设AC∩BD=O,由∠ABD=45°,∠ACD=30°,结合正弦定理可得OD与OC,OB与OA的比例关系,再由AC=4可求BD的长;
对于B、C,由已知结合三角形全等的条件可确定梯形ABCD,梯形确定,则BD长度确定;
对于D,CD的长度一定,∠ABD、∠ACD的大小一定,但AC、BD的长度可以变化,只要保证变化过程中满足AB∥CD,四边形ABCD就是梯形,∴BD长度不能确定.
故选:D.
对于B、C,由已知结合三角形全等的条件可确定梯形ABCD,梯形确定,则BD长度确定;
对于D,CD的长度一定,∠ABD、∠ACD的大小一定,但AC、BD的长度可以变化,只要保证变化过程中满足AB∥CD,四边形ABCD就是梯形,∴BD长度不能确定.
故选:D.
点评:本题考查了三角形的解法,是比较有创意的问题,解答该题的关键是多思少算,避免对每一种情况都进行计算,是中档题.

练习册系列答案
相关题目
已知圆的方程式x2+y2=36,记过点P(1,2)的最长弦和最短弦分别为AB、CD,则直线AB、CD的斜率之和等于( )
| A、-1 | ||
B、
| ||
| C、1 | ||
D、-
|
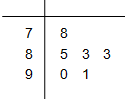 为了了解某同学的数学学习情况,对他的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,则下列关于该同学数学成绩的说法正确的是( )
为了了解某同学的数学学习情况,对他的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,则下列关于该同学数学成绩的说法正确的是( )| A、中位数为83 |
| B、平均数为85 |
| C、众数为85 |
| D、方差为19 |
班级需要在甲、乙、丙三位同学中随机的抽取两位参加一项活动,则正好抽到的是甲乙的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,棱长为2的正方体ABCD-A1B1C1D1中,E为棱C1D1上的动点,F为棱BC的中点.
如图,棱长为2的正方体ABCD-A1B1C1D1中,E为棱C1D1上的动点,F为棱BC的中点.