题目内容
11.在整数集Z中,被5所除得余数为k的所有整数组成一个“类”,记为[k],即[k]={5n+k|n∈Z},k=0,1,2,3,4;给出四个结论:(1)2015∈[0];(2)-3∈[3];(3)Z=[0]∪[1]∪[2]∪[3]∪[4];(4)“整数a,b属于同一“类”的充要条件是“a-b∈[0]”.
其中正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据新定义,对每一项进行判断即可.
解答 解:∵2015÷5=403…0,∴2015∈[0],故(1)正确;
∵-3=5×(-1)+2,∴-3∉[3],故(2)错误;
∵整数集中的数被5除的数可以且只可以分成五类,故Z=[0]∪[1]∪[2]∪[3]∪[4],故(3)正确;
∵整数a,b属于同一“类”,∴整数a,b被5除的余数相同,从而a-b被5除的余数为0,
反之也成立,故“整数a,b属于同一“类”的充要条件是“a-b∈[0]”.故(4)正确.
故选C.
点评 本题考察了对新定义的理解和运用能力.属于基础题.

练习册系列答案
相关题目
16.长方体ABCD-A1B1C1D1相邻的三个面的对角线长分别是1,2,3,则该长方外接球的面积是( )
| A. | 7π | B. | 14π | C. | 28π | D. | 36π |
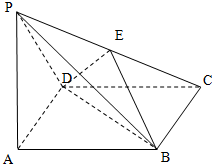 在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,PA=AB,E是PC的中点.
在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,PA=AB,E是PC的中点.