题目内容
2．
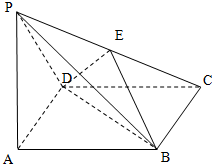在四棱锥P-ABCD中，底面ABCD是正方形，PA⊥平面ABCD，PA=AB，E是PC的中点．（1）求证：平面EBD⊥平面ABCD；
（2）求二面角E-BC-A的大小．
分析 （1）设AC∩BD=O，推导出OE∥PA，由此能证明平面EBD⊥平面ABCD．
（2）取线段BC的中点F，连接OF，EF，推导出∠EFO是二面角E-BC-A的平面角，由此能求出二面角E-BC-A的大小．
解答 证明：（1）设AC∩BD=O，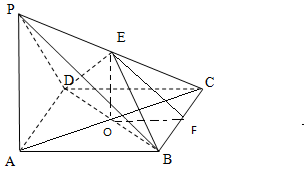
∵底面ABCD是正方形，∴O是AC中点，
∵E，O分别为线段PC，AC的中点
∴OE∥PA，
∵PA⊥平面ABCD∴OE⊥平面ABCD
∵OE?平面BDEPABCDE
∴平面EBD⊥平面ABCD…（6分）
解：（2）取线段BC的中点F，连接OF，EF
∵ABCD是正方形，F是线段BC的中点O
∴OF⊥平面BCF，
∵OE⊥平面ABCD，
∴OE⊥BC，∴BC⊥平面OEF
∴EF⊥BC，∴∠EFO是二面角E-BC-A的平面角，…（9分）
在直角三角形OEF中，OE=OF，
∴∠EFO=45°，即二面角E-BC-A的大小为45°．…（12分）
点评 本题考查面面垂直的证明，考查二面角的大小的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
名校课堂系列答案
相关题目
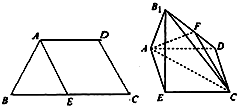如图，已知四边形ABCD满足AD∥BC，AB=AD=CD=$\frac{1}{2}$BC=2，E是BC的中点，将△BAE沿AE折成△B1AE，使面B1AE⊥面AECD，F为棱B1D上一点．