题目内容
16.长方体ABCD-A1B1C1D1相邻的三个面的对角线长分别是1,2,3,则该长方外接球的面积是( )| A. | 7π | B. | 14π | C. | 28π | D. | 36π |
分析 设出长方体的同一顶点的三条棱为a,b,c,利用对角线AC1在各个面上的投影分别是长为1,2,3的线段,求出长方体的对角线长,就是球的直径,即可求出球的表面积.
解答 解:设长方体的同一顶点的三条棱为a,b,c,对角线AC1在各面上的投影为面对角线长,
故a2+b2+c2=$\frac{{1}^{2}+{2}^{2}+{3}^{2}}{2}$=7,R=$\frac{A{C}_{1}}{2}$=$\frac{\sqrt{7}}{2}$,
故球的表面积:S=4πR2=7π.
故选:A.
点评 本题是基础题,考查长方体的外接球的表面积,考查空间想象能力,长方体的对角线长就是外接球的直径,是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.已知O为△ABC的外心,AB=3,AC=4,$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,且2x+y=1(x,y≠0),则cos∠BAC=( )
| A. | $\frac{3}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
5.已知函数f(x)=x+$\frac{1}{x}$,下列结论正确的是( )
| A. | x=-1是f(x)的极小值点 | B. | x=1是f(x)的极大值点 | ||
| C. | (1,+∞)是f(x)的单调增区间 | D. | (-1,1)是f(x)的单调增区间 |
6.直线l:y=kx+1与抛物线y2=4x恰有一个公共点,则实数k的值为( )
| A. | 0 | B. | 1 | C. | -1或0 | D. | 0或1 |
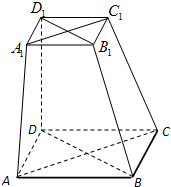 如图,在六面体中ABCD-A1B1C1D1,四边形ABCD是边长为2的正方形,四边形A1B1C1D1是边长为1的正方形,DD1⊥平面A1B1C1D1,DD1⊥平面ABCD,DD1=2.
如图,在六面体中ABCD-A1B1C1D1,四边形ABCD是边长为2的正方形,四边形A1B1C1D1是边长为1的正方形,DD1⊥平面A1B1C1D1,DD1⊥平面ABCD,DD1=2.