题目内容
1.已知函数f(x)=2x3-3x2-f′(0)x+c(c∈R),其中f(0)为函数f(x)在x=0处的导数.(1)求函数f(x)的递减区间;
(2)若函数f(x)的极大值和极小值互为相反数,求函数f(x)的解析式.
分析 (1)f′(x)=6x2-6x-f′(0),令x=0得f′(0)=0,令f′(x)<0,解得x范围可得函数f(x)的递减区间.
(2)由(1)可得:函数f(x)在(-∞,0)上递增,在(0,1)上递减,在(1,+∞)上递增,可得f(x)极小值=f(1),f(x)极大值=f(0),列出方程即可得出.
解答 解:(1)f′(x)=6x2-6x-f′(0),
令x=0得f′(0)=0-f′(0)⇒f′(0)=0,
∴f′(x)=6x2-6x,
令f′(x)<0,解得0<x<1,
∴函数f(x)的递减区间为(0,1).
(2)由(1)可得:函数f(x)在(-∞,0)上递增,在(0,1)上递减,在(1,+∞)上递增,
∴f(x)极小值=f(1)=2-3+c,f(x)极大值=f(0)=c,
∴2-3+c+c=0,
解得$c=\frac{1}{2}$.
∴f(x)=2x3-3x2+$\frac{1}{2}$.
点评 本题考查了利用导数研究函数的单调性极值,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
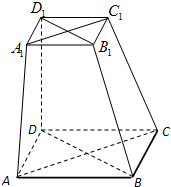 如图,在六面体中ABCD-A1B1C1D1,四边形ABCD是边长为2的正方形,四边形A1B1C1D1是边长为1的正方形,DD1⊥平面A1B1C1D1,DD1⊥平面ABCD,DD1=2.
如图,在六面体中ABCD-A1B1C1D1,四边形ABCD是边长为2的正方形,四边形A1B1C1D1是边长为1的正方形,DD1⊥平面A1B1C1D1,DD1⊥平面ABCD,DD1=2.