题目内容
已知曲线ax2+by2=12的两条动弦MA,MB所在直线的斜率分别为k1,k2.
(1)已知a=b=3且A(-2,0),B(2,0),试证明:k1k2为定值.
(2)已知a=3,b=4.
①若A(-2,0),B(2,0),试判断k1k2是否为定值?若是,求出定值;若不是,请说明理由.
②若定点M(1,-
)且k1k2=-
,试判断直线AB是否过一定点?若是,求出定点坐标;若不是,请说明理由.
(1)已知a=b=3且A(-2,0),B(2,0),试证明:k1k2为定值.
(2)已知a=3,b=4.
①若A(-2,0),B(2,0),试判断k1k2是否为定值?若是,求出定值;若不是,请说明理由.
②若定点M(1,-
| 3 |
| 2 |
| 3 |
| 4 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)当a=b=3时,ax2+by2=12为x2+y2=4,由此能证明k1k2=-1为定值.
(2)①a=3,b=4时,曲线为
+
=1,设M(x0,y0),则
+
=1,k1=
,k2=
,由此能求出k1k2=
=-
为定值.
②定点M(1,-
)且k1k2=-
,设A(x1,y1),B(x2,y2),k1k2=
•
=-
,设直线AB为y=kx+b,联立
,得(3+4k2)x2+8kbx+4b2-12=0,由此利用韦达定理能证明直线AB过一定点(0,0).
(2)①a=3,b=4时,曲线为
| x2 |
| 4 |
| y2 |
| 3 |
| x02 |
| 4 |
| y02 |
| 3 |
| y0 |
| x0+2 |
| y0 |
| x0-2 |
| y02 |
| x02-4 |
| 3 |
| 4 |
②定点M(1,-
| 3 |
| 2 |
| 3 |
| 4 |
y1+
| ||
| x1-1 |
y2+
| ||
| x2-1 |
| 3 |
| 4 |
|
解答:
(1)证明:当a=b=3时,ax2+by2=12为x2+y2=4,
它是以(0,0)为圆心,以2为半径的圆,
此时A(-2,0),B(2,0)是圆的两个端点,
∴由圆的性质得MA⊥MB,
∴k1k2=-1为定值.
(2)①解:a=3,b=4时,曲线为
+
=1,
且A(-2,0),B(2,0)为椭圆长轴两端点,
设M(x0,y0),则
+
=1,
∵弦MA,MB所在直线的斜率分别为k1,k2,
∴k1=
,k2=
,
∴k1k2=
=-
为定值.
②定点M(1,-
)且k1k2=-
,
设A(x1,y1),B(x2,y2),k1=
,k2=
,
k1k2=
•
=-
,(*)
设直线AB为y=kx+b,
联立
,得(3+4k2)x2+8kbx+4b2-12=0,
∴x1+x2=-
,x1x2=
,y1+y2=k(x1+x2)+2b,
y1y2=k2x1x2+k(x1+x2)+b2,
代入(*)式,解得b=0,
∴直线AB的方程为y=kx,
∴直线AB过一定点(0,0).
它是以(0,0)为圆心,以2为半径的圆,
此时A(-2,0),B(2,0)是圆的两个端点,
∴由圆的性质得MA⊥MB,
∴k1k2=-1为定值.
(2)①解:a=3,b=4时,曲线为
| x2 |
| 4 |
| y2 |
| 3 |
且A(-2,0),B(2,0)为椭圆长轴两端点,
设M(x0,y0),则
| x02 |
| 4 |
| y02 |
| 3 |
∵弦MA,MB所在直线的斜率分别为k1,k2,
∴k1=
| y0 |
| x0+2 |
| y0 |
| x0-2 |
∴k1k2=
| y02 |
| x02-4 |
| 3 |
| 4 |
②定点M(1,-
| 3 |
| 2 |
| 3 |
| 4 |
设A(x1,y1),B(x2,y2),k1=
y1+
| ||
| x1-1 |
y2+
| ||
| x2-1 |
k1k2=
y1+
| ||
| x1-1 |
y2+
| ||
| x2-1 |
| 3 |
| 4 |
设直线AB为y=kx+b,
联立
|
∴x1+x2=-
| 8kb |
| 3+4k2 |
| 4b2-12 |
| 3+4k2 |
y1y2=k2x1x2+k(x1+x2)+b2,
代入(*)式,解得b=0,
∴直线AB的方程为y=kx,
∴直线AB过一定点(0,0).
点评:本题考查两直线的斜率这积为定值的证明,考查直线是事过定点的判断与求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
在△ABC中,A=30°,B=60°,a=10,则b等于( )
| A、20 | ||||
B、10
| ||||
C、
| ||||
D、5
|
满足{1}⊆M⊆{1,2,3,4,5}的集合M的个数为( )
| A、4 | B、6 | C、8 | D、16 |
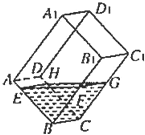 如图,在透明材料制成的长方体容器ABCD-A1B1C1D1内灌注一些水,固定容器底面一边BC于桌面上,再将容器倾斜根据倾斜度的不同,有下列命题:
如图,在透明材料制成的长方体容器ABCD-A1B1C1D1内灌注一些水,固定容器底面一边BC于桌面上,再将容器倾斜根据倾斜度的不同,有下列命题: