题目内容
14.点P(-1,2,3)关于xOz平面对称的点的坐标是(-1,-2,3).分析 利用点(x,y,z)关于xoz平面的对称点为(x,-y,z)即可得出.
解答 解:P(-1,2,3)关于xoz平面的对称点为(-1,-2,3).
故答案为(-1,-2,3).
点评 本题考查了关于坐标平面对称点的性质,考查了推理能力,属于基础题.

练习册系列答案
相关题目
4.“a>1”是“函数f(x)=(a2)x在定义域内是增函数”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.函数f(x)=aex-1-$\sqrt{x}$+1的图象在点(1,f(1))处的切线斜率为$\frac{5}{2}$,则实数a=( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 3 | D. | -3 |
6.若实数 x,y满足 (x-2)2+y2=1,则$\frac{y}{x}$的最大值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{3}$ |
3.设f(x)=x3+ax2+bx+1的导数f'(x)满足f'(1)=2a,f'(2)=-b,其中常数a,b∈R.
(Ⅰ)求曲线y=f(x);
(Ⅱ) 设g(x)=f'(x)e-x,求函数g(x)的极值.
(Ⅰ)求曲线y=f(x);
(Ⅱ) 设g(x)=f'(x)e-x,求函数g(x)的极值.
4.不等式x2-2|x|-3<0的解集是( )
| A. | (-3,3) | B. | (-3,1) | C. | (-3,0)∪(0,3) | D. | (-1,0)∪(0,1) |
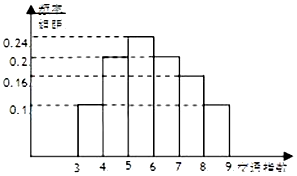 交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围为[0,10],分为五个级别,T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如右图.
交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围为[0,10],分为五个级别,T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如右图.