题目内容

在△ABC中，若|
AB
|=2，|
AC
|=3，∠BAC=60°，则
BA
•
BC
=
 
．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用数量积的定义即可得出．
解答： 解：∵|
AB
|=2，|
AC
|=3，∠BAC=60°，
则
BA
•
BC
=2×3×cos60°=3．
故答案为：3．
点评：本题查克拉数量积的运算性质，属于基础题．
练习册系列答案
相关题目
已知
OA
=(1，0)，
OC
=（-1，
3
），
CB
=（cosα，sinα），则
OA
与
OB
的夹角的取值范围是
 
．
已知等比数列{an}的前n项和为Sn，则下列选项中一定成立的是（　　）
A、若a1＞0，则a2015＜0
B、若a2＞0，则a2016＜0
C、若a1＞0，则S2015＞0
D、若a2＞0，则S2016＞0
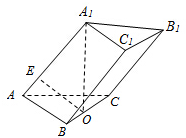在三棱柱ABC-A1B1C1中，已知AA1=8，AC=AB=5，BC=6，点A1在底面ABC的射影是线段BC的中点O，在侧棱AA1上存在一点E，且OE⊥B1C．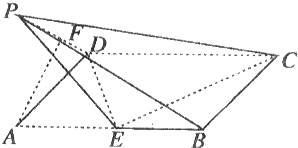
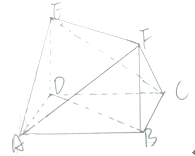（1）求证：OE⊥面BB1C1C；
（2）求平面A1B1C与平面B1C1C所成锐二面角的余弦值的大小．
如图所示，在矩形ABCD中，AD=1，AB=2，点 E是线段AB的中点，把三角形AED沿DE折起，设折起后点 A的位置为P，F是PD的中点．
（1）求证：无论P在什么位置，都有AF∥平面PEC；
（2）当点 P在平面ABCD上的射影落在线段DE上时，求二面角P-EC-D的余弦值．
已知三角形ABC中，AB=AC，BC=4，∠BAC=120°，
BE
=3
EC
，若P是BC边上的动点，则
AP
•
AE
的取值范围是
 
．
如图，多面体ABCDEF中，底面ABCD是菱形，∠BCD=60°，四边形BDEF是正方形且DE⊥平面ABCD．
（Ⅰ）求证：CF∥平面ADE；
（Ⅱ）若AE=
2
，求多面体ABCDEF的体积V．
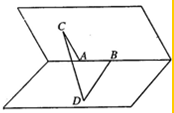如图，60°的二面角的棱上有A，B两点，线段AC，BD分别在这个二面角的两个半平面内，且AC⊥AB，BD⊥AB，已知AB=4，AC=6，BD=8．
（1）用向量
BD
、
AB
、
CA
表示
CD
；
（2）求|
CD
|的值．
平面向量
a
，
b
满足|
a
|=2，|
a
+
b
|=4，且向量
a
与向量
a
+
b
的夹角为
π
3
，则|
b
|为（　　）
A、2
B、2
3
C、2
5
D、2
5-2
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网