题目内容
12．
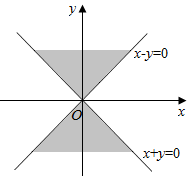给出三个不等式：①x2-y2＞0；②x2-y2＜0；③x2+y2＞0，如图所示的阴影区域应是序号为②的不等式所表示的平面区域．
分析 根据不等式的等价条件，进行转化，作出对应的平面区域即可得到结论．
解答 解：：①x2-y2＞0等价为（x-y）（x+y＞0，即$\left\{\begin{array}{l}{x-y＞0}\\{x+y＞0}\end{array}\right.$或$\left\{\begin{array}{l}{x-y＜0}\\{x+y＜0}\end{array}\right.$
②x2-y2＜0等价为（x-y）（x+y）＜0；即$\left\{\begin{array}{l}{x-y＞0}\\{x+y＜0}\end{array}\right.$或$\left\{\begin{array}{l}{x-y＜0}\\{x+y＞0}\end{array}\right.$
③x2+y2＞0恒成立，
则不等式②对应的区域是如图对应的区域，
故答案为：②．
点评 本题主要考查平面区域的作法，根据二元一次不等式组与平面区域的关系是解决本题的关键．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
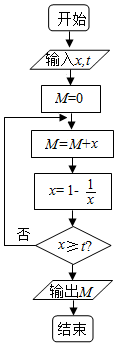
2．执行如图所示的程序框图，如果输入的x=t=3，则输出的M等于（ ）
| A． | 3 | B． | $\frac{11}{3}$ | C． | $\frac{19}{6}$ | D． | $\frac{37}{6}$ |
3．若执行如图所示的程序框图，输入x1=1，x2=2，x3=3，$\overline{x}$=2，则输出的数S等于（ ）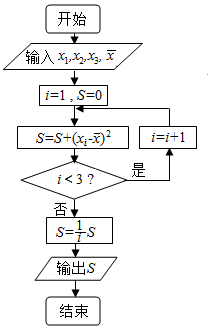
| A． | $\frac{2}{3}$ | B． | 1 | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |