题目内容
4.是否存在实数x,使得(x+$\sqrt{3}$i)3=log${\;}_{\sqrt{3}}$$\frac{1}{81}$成立?如果存在,求出x的值;如果不存在,请说明理由.分析 由对数运算知log${\;}_{\sqrt{3}}$$\frac{1}{81}$=-8,从而化简可得x3+3x($\sqrt{3}$i)2+3x2$\sqrt{3}$i+($\sqrt{3}$i)3=-8,从而解得.
解答 解:由对数运算知,log${\;}_{\sqrt{3}}$$\frac{1}{81}$=-8,
故(x+$\sqrt{3}$i)3=-8,
即x3+3x($\sqrt{3}$i)2+3x2$\sqrt{3}$i+($\sqrt{3}$i)3=-8,
即x3-9x+3x2$\sqrt{3}$i-3$\sqrt{3}$i=-8,
故$\left\{\begin{array}{l}{{x}^{3}-9x=-8}\\{3\sqrt{3}{x}^{2}-3\sqrt{3}=0}\end{array}\right.$,
解得,x=1.
点评 本题考查了对数运算的应用及复数相等的应用,属于基础题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
15.一个几何体的三视图如图,则该几何体的体积为( )
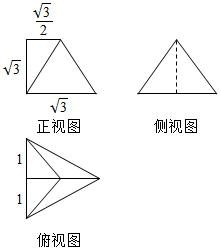

| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
16.设△ABC内角A,B,C的对边分别为a,b,c,已知bc=60,S△ABC=15$\sqrt{3}$.则A为( )
| A. | 30° | B. | 60° | C. | 60°或120° | D. | 30°或150° |
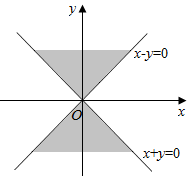 给出三个不等式:①x2-y2>0;②x2-y2<0;③x2+y2>0,如图所示的阴影区域应是序号为②的不等式所表示的平面区域.
给出三个不等式:①x2-y2>0;②x2-y2<0;③x2+y2>0,如图所示的阴影区域应是序号为②的不等式所表示的平面区域.