题目内容
7.已知函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{3}x|,0<x<3}\\{sin(\frac{π}{2}x-π),3≤x≤7}\end{array}\right.$,若存在实数a,b,c,d,满足f(a)=f(b)=f(c)=f(d),其中0<a<b<c<d,则a+b+c+d的取值范围是(12,$\frac{40}{3}$).分析 先画出函数f(x)的图象,再根据条件利用对数函数的运算性质以及三角函数的对称性,利用数形结合,即可求出其范围.
解答  解:函数f(x)的图象如下图所示:
解:函数f(x)的图象如下图所示:
若a、b、c、d互不相同,且f(a)=f(b)=f(c)=f(d),
∵a<b<c<d,
∴0<a<1,1<b<3,
则由f(a)=f(b)得log3a=-log3b,即log3a+log3b=log3ab=0
则ab=1,
由|log3a|=1得log3a=-1,则a=$\frac{1}{3}$,
即$\frac{1}{3}$<a<1,
同时c∈(3,4),d∈(6,7),
∵c,d关于x=5对称,∴$\frac{c+d}{2}$=5,
则c+d=10,则10=c+d则a+b+c+d=a+b+10=a+$\frac{1}{a}$+10,
∵a+$\frac{1}{a}$在$\frac{1}{3}$<a<1上为减函数,
∴2<a+$\frac{1}{a}$<$\frac{10}{3}$,
则12<a+$\frac{1}{a}$+10<$\frac{40}{3}$,
即a+b+c+d的取值范围是(12,$\frac{40}{3}$),
故答案为:(12,$\frac{40}{3}$)
点评 本题考查的知识点是分段函数的应用,由题意正确画出图象和熟练掌握对数函数的图象是解题的关键.利用对数函数的运算性质以及三角函数的对称性进行转化是解决本题的关键.

练习册系列答案
相关题目
18.若$\overrightarrow{a}$=(2,3,m),$\overrightarrow{b}$=(2n,6,8)且$\overrightarrow{a}$,$\overrightarrow{b}$为共线向量,则m+n的值为( )
| A. | 7 | B. | $\frac{5}{2}$ | C. | 6 | D. | 8 |
15.一个几何体的三视图如图,则该几何体的体积为( )
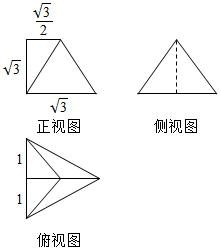

| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
16.设△ABC内角A,B,C的对边分别为a,b,c,已知bc=60,S△ABC=15$\sqrt{3}$.则A为( )
| A. | 30° | B. | 60° | C. | 60°或120° | D. | 30°或150° |
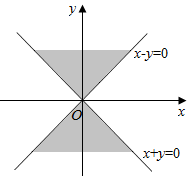 给出三个不等式:①x2-y2>0;②x2-y2<0;③x2+y2>0,如图所示的阴影区域应是序号为②的不等式所表示的平面区域.
给出三个不等式:①x2-y2>0;②x2-y2<0;③x2+y2>0,如图所示的阴影区域应是序号为②的不等式所表示的平面区域.