题目内容
2.已知a+b≠0,证明a2+b2-a-b+2ab=0成立的充要条件是a+b=1.分析 根据充要条件的定义分别证明充分性和必要性成立即可.
解答 证明:先证充分性:
若a+b=1,
则a2+b2-a-b+2ab=(a+b)2-(a+b)=1-1=0,即充分性成立,
必要性:
若a2+b2-a-b+2ab=0则(a+b)2-(a+b)=(a+b)(a+b-1)=0,
∵a+b≠0,∴a+b-1=0,
即a+b=1,成立,
综上a2+b2-a-b+2ab=0成立的充要条件是a+b=1
点评 本题主要考查充分条件和必要条件的证明,根据充要条件的定义证明充分性和必要性是解决本题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
2.已知直线l1:x-my+2=0,直线l2的方向向量$\overrightarrow{a}$=(-1,-2),若l1⊥l2,则m的值为( )
| A. | -$\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | -2 |
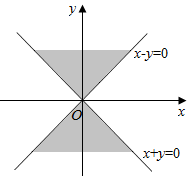 给出三个不等式:①x2-y2>0;②x2-y2<0;③x2+y2>0,如图所示的阴影区域应是序号为②的不等式所表示的平面区域.
给出三个不等式:①x2-y2>0;②x2-y2<0;③x2+y2>0,如图所示的阴影区域应是序号为②的不等式所表示的平面区域.