题目内容
18.已知某几何体的三视图如图所示,则该几何体的表面积为( )
| A. | 40 | B. | 30 | C. | 36 | D. | 42 |
分析 根据三视图判断几何体是长方体削去一个三棱锥,截面三角形为等腰三角形,根据长方体的边长计算截面三角形的边长,求出截面的面积,再求几何体的其他各面的面积,然后相加.
解答  解:由三视图知几何体是长为4,宽为2,高为2的长方体削去一个三棱锥,其直观图如图:
解:由三视图知几何体是长为4,宽为2,高为2的长方体削去一个三棱锥,其直观图如图:
截面三角形为等腰三角形,腰长为$\sqrt{16+4}$=2$\sqrt{5}$,底边长为2$\sqrt{2}$,
∴截面的面积为$\frac{1}{2}$×2$\sqrt{2}$×$\sqrt{20-2}$=6,
∴几何体的表面积S=4×2+$\frac{1}{2}$×4×2+$\frac{1}{2}$×2×2+2×2+4×2+$\frac{1}{2}$×4×2+6=36.
故选:C.
点评 本题考查了由三视图求几何体的表面积,解答此类问题的关键是判断几何体的形状及数据所对应的几何量.

练习册系列答案
相关题目
3.已知集合A={-2,0,2},B={x|x2-x-2=0},则A∩B=( )
| A. | ∅ | B. | {0} | C. | {2} | D. | {-2} |
10.己知函数y=f(x)-2x是偶函数,且f(1)=2,则f(-1)=( )
| A. | 2 | B. | -2 | C. | 0 | D. | 1 |
8.新高考政策已经在上海和浙江试验实施.为了解学生科目选择的意向,从某校高一学生中随机抽取30位同学,对其选课情况进行统计分析,得到频率分布表如下:
(Ⅰ)若所抽取的30位同学中,有2位同学选择了“历史、地理、生物”组合,3位同学选择了“物理、政治、历史”组合.求a、b、c的值;
(Ⅱ)在(Ⅰ)的条件下,将选择了“历史、地理、生物”组合的2位同学记为x1、x2,选择了“物理、政治、历史”组合的3位同学记为y1、y2、y3.现从这5位同学中任取2位(假定每位同学被抽中的可能性相同),写出所有可能的结果,并求这两位同学科目选择恰好相同的概率.
| 科目选择 | 物理 化学 生物 | 历史 地理 政治 | 物理 化学 地理 | 历史 地理 生物 | 物理 政治 历史 | 其他 |
| 频率 | $\frac{1}{5}$ | $\frac{1}{6}$ | $\frac{2}{15}$ | a | b | c |
(Ⅱ)在(Ⅰ)的条件下,将选择了“历史、地理、生物”组合的2位同学记为x1、x2,选择了“物理、政治、历史”组合的3位同学记为y1、y2、y3.现从这5位同学中任取2位(假定每位同学被抽中的可能性相同),写出所有可能的结果,并求这两位同学科目选择恰好相同的概率.
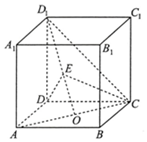 (理科)如图,在正方体ABCD-A1B1C1D1,O是AC的中点,E是线段D1O上一点,且$\frac{{D}_{1}E}{EO}$=λ.
(理科)如图,在正方体ABCD-A1B1C1D1,O是AC的中点,E是线段D1O上一点,且$\frac{{D}_{1}E}{EO}$=λ.