题目内容
6.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点F作圆x2+y2=a2的切线,切点为M,延长FM交双曲线右支于点P,若M为FP的中点,则双曲线的离心率是$\sqrt{5}$.分析 作出简图,由图中可得线段的长,从而得到b=2a,进而求双曲线的离心率.
解答  解:如图|OF|=c,|OM|=a,|FG|=2c;
解:如图|OF|=c,|OM|=a,|FG|=2c;
∴|F|=b,又∵M为PF的中点,
|PG|=2|OM|=2a,
|PF|=2b,
∴|PF|-|PG|=2b-2a=2a;
∴b=2a,
∴c=$\sqrt{5}$a,
∴e=$\frac{c}{a}$=$\sqrt{5}$.
故答案为$\sqrt{5}$.
点评 本题考查了学生的作图能力及分析转化的能力,考查了学生数形结合的思想应用,同时考查了双曲线的定义,属于中档题.

练习册系列答案
相关题目
16.设Sn为等差数列{an}的前n项的和a1=1,$\frac{{{S_{2017}}}}{2017}-\frac{{{S_{2015}}}}{2015}=1$,则数列$\left\{{\frac{1}{S_n}}\right\}$的前2017项和为( )
| A. | $\frac{2017}{1009}$ | B. | $\frac{2017}{2018}$ | C. | $\frac{1}{2017}$ | D. | $\frac{1}{2018}$ |
18.已知某几何体的三视图如图所示,则该几何体的表面积为( )


| A. | 40 | B. | 30 | C. | 36 | D. | 42 |
15.对任意实数a,b,定义运算“⊕”:$a⊕b=\left\{\begin{array}{l}b,a-b≥1\\ a,a-b<1\end{array}\right.$,设f(x)=(x2-1)⊕(4+x),若函数y=f(x)-k有三个不同零点,则实数k的取值范围是( )
| A. | (-1,2] | B. | [0,1] | C. | [-1,3) | D. | [-1,1) |
16.已知集合A={-1,1,2,3},B={x|x≥2},那么A∩B等于( )
| A. | {3} | B. | {2,3} | C. | {-1,2,3} | D. | {-1,1,2,3} |
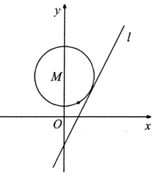 已知直线l:y=2x+n,n∈R,圆M的圆心在y轴,且过点(1,1).
已知直线l:y=2x+n,n∈R,圆M的圆心在y轴,且过点(1,1).