题目内容
3.已知集合A={-2,0,2},B={x|x2-x-2=0},则A∩B=( )| A. | ∅ | B. | {0} | C. | {2} | D. | {-2} |
分析 直接求解一元二次方程得集合B,再利用交集的运算性质求解得答案.
解答 解:由集合A={-2,0,2},B={x|x2-x-2=0}={-1,2},
则A∩B═{-2,0,2}∩{-1,2}={2}.
故选:C.
点评 本题考查了交集及其运算,考查了一元二次方程的解法,是基础题.

练习册系列答案
相关题目
18.已知某几何体的三视图如图所示,则该几何体的表面积为( )


| A. | 40 | B. | 30 | C. | 36 | D. | 42 |
8.设集合U=R,集合$A=\left\{{x\left|{{{log}_2}x<1}\right.}\right\},B=\left\{{x\left|{{x^2}-2x-3≤0}\right.}\right\}$,则(∁UA)∩B=( )
| A. | [2,3] | B. | [-1,2] | C. | [-1,0] | D. | [-1,0]∪[2,3] |
15.对任意实数a,b,定义运算“⊕”:$a⊕b=\left\{\begin{array}{l}b,a-b≥1\\ a,a-b<1\end{array}\right.$,设f(x)=(x2-1)⊕(4+x),若函数y=f(x)-k有三个不同零点,则实数k的取值范围是( )
| A. | (-1,2] | B. | [0,1] | C. | [-1,3) | D. | [-1,1) |
12.在△ABC中,a,b,c分别是A,B,C的对边,$a=2\sqrt{3},b=2\sqrt{2}$,且1+2cos(B+C)=0,则BC边上的高等于( )
| A. | $2({\sqrt{3}+1})$ | B. | $2({\sqrt{3}-1})$ | C. | $\sqrt{3}+1$ | D. | $\sqrt{3}-1$ |
13.实数x,y满足$\left\{\begin{array}{l}x≤3\\ x+y≥0\\ x-y+6≥0.\end{array}\right.$若z=ax+y的最大值为3a+9,最小值为3a-3,则a的取值范围是( )
| A. | [-1,0] | B. | [0,1] | C. | [-1,1] | D. | (-∞,-1]∪[1,+∞) |
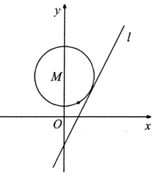 已知直线l:y=2x+n,n∈R,圆M的圆心在y轴,且过点(1,1).
已知直线l:y=2x+n,n∈R,圆M的圆心在y轴,且过点(1,1).