题目内容
7.已知等比数列{an}的前n项和为Sn,a1=1,S6=9S3.(Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=1+log2an,求数列{bn}的前n项和.
分析 (Ⅰ)设等比数列{an}的公比为q,运用等比数列的求和公式,求得q=2,再由等比数列的通项公式即可得到;
(Ⅱ)运用对数的性质化简bn=n,再由等差数列的求和公式,计算即可得到.
解答 解:(Ⅰ)设等比数列{an}的公比为q,
a1=1,S6=9S3,知q≠1,
故有$\frac{1-{q}^{6}}{1-q}$=$\frac{9(1-{q}^{3})}{1-q}$,
即(1-q3)(1+q3)=9(1-q3),
即有1+q3=9,即q3=8,解得q=2,
则an=a1qn-1=2n-1;
(Ⅱ)bn=1+log2an=1+log22n-1=1+n-1=n,
则数列{bn}的前n项和为1+2+…+n=$\frac{1}{2}$n(1+n).
点评 本题考查等比数列的通项和求和公式的运用,同时考查对数的运算和等差数列的求和公式,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
10.一个几何体的三视图如图所示,该几何体的体积是( )


| A. | 12 | B. | 18 | C. | 24 | D. | 36 |
18.已知$tanθ=\frac{3}{4}$,那么$tan(θ+\frac{π}{4})$等于( )
| A. | -7 | B. | $-\frac{1}{7}$ | C. | 7 | D. | $\frac{1}{7}$ |
2. 一个几何体的三视图如图所示,则该几何体的体积等于( )
一个几何体的三视图如图所示,则该几何体的体积等于( )
 一个几何体的三视图如图所示,则该几何体的体积等于( )
一个几何体的三视图如图所示,则该几何体的体积等于( )| A. | 8+4π | B. | 8+2π | C. | 8+$\frac{4}{3}$π | D. | 8+$\frac{2}{3}$π |
12.某校学习小组开展“学生数学成绩与化学成绩的关系”的课题研究,对该校高二年级800名学生上学期期 数学和化学成绩,按优秀和不优秀分类得结果:数学和化学都优秀的有60人,数学成绩优秀但化学不优秀的有140人,化学成绩优秀但数学不优秀的有100人.
(Ⅰ)补充完整表格并判断能否在犯错概率不超过0.001前提下认为该校学生的数学成绩与化学成绩有关系?
(Ⅱ)现有4名成员甲、乙、丙、丁随机分成两组,每组2人,一组负责收集成绩,另一组负责数据处理.求学生甲分到负责收集成绩组,学生乙分到负责数据处理组的概率.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
(Ⅰ)补充完整表格并判断能否在犯错概率不超过0.001前提下认为该校学生的数学成绩与化学成绩有关系?
| 数学优秀 | 数学不优秀 | 总计 | |
| 化学优秀 | 60 | 100 | 160 |
| 化学不优秀 | 140 | 500 | 640 |
| 总计 | 200 | 600 | 800 |
| p(K2>k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
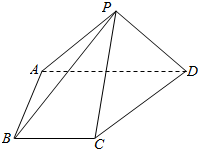 如图,四棱锥P-ABCD中,平面PAD⊥底面ABCD,PA⊥PD,PA=PD,BC∥AD,AB⊥AD,AD=2AB=2BC=2.
如图,四棱锥P-ABCD中,平面PAD⊥底面ABCD,PA⊥PD,PA=PD,BC∥AD,AB⊥AD,AD=2AB=2BC=2.