题目内容
五个人站成一排,求在下列条件下的不同排法种数:(用数字作答)
(1)甲、乙两人相邻;
(2)甲、乙两人不相邻;
(3)甲不在排头,并且乙不在排尾;
(4)甲在乙前,并且乙在丙前.
(1)甲、乙两人相邻;
(2)甲、乙两人不相邻;
(3)甲不在排头,并且乙不在排尾;
(4)甲在乙前,并且乙在丙前.
考点:排列、组合及简单计数问题
专题:排列组合
分析:(1)利用捆绑法,把甲乙二人看作一个复合元素,再和另外3的全排列.
(2)利用插空法,先排除甲乙之外的3人,形成4个空,再把甲乙插入空位即可,
(3)利用间接法,先任意排,再排除甲在排头,乙在排尾的情况,
(4)利用定序法,甲乙丙的顺序有6种,总数除以顺序数即可.
(2)利用插空法,先排除甲乙之外的3人,形成4个空,再把甲乙插入空位即可,
(3)利用间接法,先任意排,再排除甲在排头,乙在排尾的情况,
(4)利用定序法,甲乙丙的顺序有6种,总数除以顺序数即可.
解答:
解:(1)把甲、乙看成一个人来排有
种,而甲、乙也存在顺序变化,所以甲、乙相邻排法种数为
•
=48种,
(2)排除甲乙之外的3人,形成4个空,再把甲乙插入空位有
=72,
(3)甲不在排头,并且乙不在排尾排法种数为:
-2
+
=78种,
(4)因为甲、乙、丙共有3!种顺序,所以甲在乙前,并且乙在丙前排法种数为:
÷3!=20种,
| A | 4 4 |
| A | 4 4 |
| A | 2 2 |
(2)排除甲乙之外的3人,形成4个空,再把甲乙插入空位有
| A | 3 3 |
| A | 2 4 |
(3)甲不在排头,并且乙不在排尾排法种数为:
| A | 5 5 |
| A | 4 4 |
| A | 3 3 |
(4)因为甲、乙、丙共有3!种顺序,所以甲在乙前,并且乙在丙前排法种数为:
| A | 5 5 |
点评:本题考查了排队问题中的几种常用的方法,审清题意,选择合理的方法是关键,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
命题“对任意x∈R,都有2x>0”的否定是( )
| A、对任意x∈R,都有2x≤0 |
| B、不存在x∈R,使得2x≤0 |
| C、存在x0∈R,使得2x>0 |
| D、存在x0∈R,2x0≤0 |
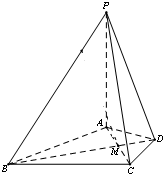 在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°.
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°.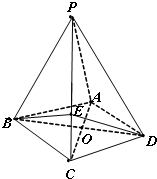 如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD.PA=AB=2,∠BAD=120°,E是PC上的一点,且BE与平面PAB所成角的正弦值为
如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD.PA=AB=2,∠BAD=120°,E是PC上的一点,且BE与平面PAB所成角的正弦值为