题目内容

10名学生分成3组，其中一组4人，另两组3人但正副班长不能分在同一组，有多少种不同的分组方法？
考点：计数原理的应用
专题：排列组合
分析：利用间接法，先求出没有要求的分组种数，再排除两个班长在同一组的种数，问题得以解决．
解答： 解：先算出10个人排433的方法，有
C
4
10
•
C
3
6
•
C
3
3
A
2
2
=2100种，
再减去两个班长在同一组的可能，就是其他8人按照233，413 两种方式分组，有
C
2
8
•
C
3
6
•C
3
3
A
2
2
+
C
4
8
•
C
1
4
•
C
3
3
=560，
故10名学生分成3组，其中一组4人，另两组3人但正副班长不能分在同一组，有2100-560=1540种不同的分组方法．
点评：本题主要考查了分组的问题，合理分组时关键，属于中档题．
练习册系列答案
相关题目
已知an=n（n+1），以下四个数中，哪个是数列{an}中的一项（　　）
A、18B、21C、25D、30
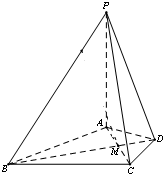在四棱锥P-ABCD中，PA⊥平面ABCD，△ABC是正三角形，AC与BD的交点M恰好是AC中点，又PA=AB=4，∠CDA=120°．
（1）求证：BD⊥PC；
（2）求二面角D-PC-B的余弦值．
已知各项均不相等的等差数列{an}的前四项和S4=14，且a1，a3，a7成等比数列．
（1）求数列{an}的通项公式；
（2）设Tn为数列{
1
anan+1
}的前n项和，若Tn≥λ对?n∈N*恒成立，求实数λ的最大值．
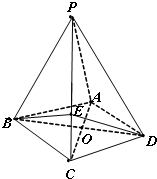如图，四棱锥P-ABCD中，底面ABCD为菱形，PA⊥底面ABCD．PA=AB=2，∠BAD=120°，E是PC上的一点，且BE与平面PAB所成角的正弦值为
3
4
．
（1）证明：E为PC的中点；
（2）求二面角A-BE-C的大小．
已知a，b∈R，若矩阵A=
-1a
b3
所对应的变换TA把直线l：2x-y=3变换为它自身．
（Ⅰ）求矩阵A；
（Ⅱ）求矩阵A的逆矩阵．
某学校为响应省政府号召，每学期派老师到各个民工子弟学校支教，以下是该学校50名老师上学期在某一个民工子弟学校支教的次数统计结果：
支教次数0123
人数5102015
根据上表信息解答以下问题：
（1）从该学校任选两名老师，用η表示这两人支教次数之和，记“函数f（x）=x2-ηx-1在区间（4，5）上有且只有一个零点”为事件A，求事件A发生的概率P1；
（2）从该学校任选两名老师，用ξ表示这两人支教次数之差的绝对值，求随机变量ξ的分布列及数学期望Eξ．
在△ABC中，BC=a，AC=b，不等式x2-2
3
x+2≤0的解集为{x|a≤x≤b}，且2cos（A+B）=1．求：
（1）角C的度数；        
（2）AB的长度．
已知函数f（x）=x3+ax+b，a，b∈R的图象记为曲线E，过一点A（
1
2
，-
3
8
）作曲线E的切线，这样的切线有且仅有两条．
（Ⅰ）求a+2b的值；
（Ⅱ）若点A在曲线E上，对任意的x∈[0，1]，求证：f（x）+|a+3b+1|+
1
2
≥0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网