题目内容
已知数列{an}的前n项和是Sn,Sn=2an-1(n∈N*).
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=2n•an,求数列{bn}的前n项和Tn;
(3)若数列{cn}满足cn=3n+2(-1)n-1λan(λ为非零常数),确定λ的取值范围,使n∈N*时,都有cn+1>cn.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=2n•an,求数列{bn}的前n项和Tn;
(3)若数列{cn}满足cn=3n+2(-1)n-1λan(λ为非零常数),确定λ的取值范围,使n∈N*时,都有cn+1>cn.
考点:数列与不等式的综合,数列的求和
专题:综合题,等差数列与等比数列
分析:(1)由已知条件推导出{an}是首项为1,公比为2的等比数列,从而可求数列{an}的通项公式;
(2)用错位相减法能求出数列{bn}的前n项和Tn;
(3)条件转化为2•3n+(-1)nλ3•2n>0,分类讨论,即可确定λ的取值范围.
(2)用错位相减法能求出数列{bn}的前n项和Tn;
(3)条件转化为2•3n+(-1)nλ3•2n>0,分类讨论,即可确定λ的取值范围.
解答:
解:(1)当n=1时,a1=S1=2a1-1,∴a1=1.
当n>1时,Sn=2an-1,∴Sn-1=2an-1-1,
∴Sn-Sn-1=2an-2an-1,
∴an=2an-2an-1,
∴an=2an-1,
∴{an}是首项为1,公比为2的等比数列,∴an=2n-1,n∈N*.
(2)bn=2n•an=n•2n.
2Tn=1•2+2•22+…+n•2n,①
2Tn=1•22+2•23+…+(n-1)•2n+n•2n+1,②
①-②,得-Tn=22+23+…+2n-n•2n+1
=(1-n)•2n+1-2,
∴Tn=(n-1)•2n+1+2.
(3)∵Cn=3n+2•(-1)n+1λ2n-1=3n+(-1)n+1λ2n
∴Cn+1>Cn即 3n+1+(-1)nλ2n+1>3n+(-1)nλ2n
即3n+1-3n+(-1)nλ2n+1-(-1)n-1λ2n>0
即2•3n+(-1)nλ(2n+1+2n)>0
即2•3n+(-1)nλ3•2n>0
∴(-1)nλ>
即(-1)nλ>-(
)n-1…(8分)
当n为偶数时-(
)n-1≤-
,∴λ>-
…(10分)
当n为奇数时-(
)n-1≤-1,∴-λ>-1
即 λ<1
又∵λ≠0
∴-
<λ<1且λ≠0…(12分)
当n>1时,Sn=2an-1,∴Sn-1=2an-1-1,
∴Sn-Sn-1=2an-2an-1,
∴an=2an-2an-1,
∴an=2an-1,
∴{an}是首项为1,公比为2的等比数列,∴an=2n-1,n∈N*.
(2)bn=2n•an=n•2n.
2Tn=1•2+2•22+…+n•2n,①
2Tn=1•22+2•23+…+(n-1)•2n+n•2n+1,②
①-②,得-Tn=22+23+…+2n-n•2n+1
=(1-n)•2n+1-2,
∴Tn=(n-1)•2n+1+2.
(3)∵Cn=3n+2•(-1)n+1λ2n-1=3n+(-1)n+1λ2n
∴Cn+1>Cn即 3n+1+(-1)nλ2n+1>3n+(-1)nλ2n
即3n+1-3n+(-1)nλ2n+1-(-1)n-1λ2n>0
即2•3n+(-1)nλ(2n+1+2n)>0
即2•3n+(-1)nλ3•2n>0
∴(-1)nλ>
| -2•3n |
| 3•2n |
| 3 |
| 2 |
当n为偶数时-(
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
当n为奇数时-(
| 3 |
| 2 |
即 λ<1
又∵λ≠0
∴-
| 3 |
| 2 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
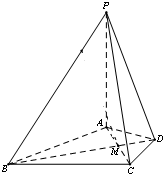 在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°.
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°.