题目内容
已知直角坐标平面内一动点P到点F(2,0)的距离与直线x=-2的距离相等.
(Ⅰ)求动点P的轨迹C的方程;
(Ⅱ)过点M(m,0)(m>0)作直线与曲线C相交于A,B两点,问:是否存在一条垂直于x轴的直线与以线段AB为直径的圆始终相切?若存在,求出m的值;若不存在,请说明理由.
(Ⅰ)求动点P的轨迹C的方程;
(Ⅱ)过点M(m,0)(m>0)作直线与曲线C相交于A,B两点,问:是否存在一条垂直于x轴的直线与以线段AB为直径的圆始终相切?若存在,求出m的值;若不存在,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:综合题,直线与圆,圆锥曲线的定义、性质与方程
分析:(Ⅰ)根据直角坐标平面内一动点P到点F(2,0)的距离与直线x=-2的距离相等,利用抛物线的定义,可求动点P的轨迹C的方程;
(Ⅱ)设过点M的直线方程为x=λy+m,代入y2=8x,求出AB,设存在直线x=x0满足条件,则2|4λ2+m-x0|=
,从而可得(16+8x0)λ2+8m-m2-x02+2mx0=0对任意的λ成立,即可得出结论.
(Ⅱ)设过点M的直线方程为x=λy+m,代入y2=8x,求出AB,设存在直线x=x0满足条件,则2|4λ2+m-x0|=
| (1+λ2)(64λ2+32m) |
解答:
解:(Ⅰ)由抛物线的定义,知所求P点的轨迹是以F(2,0)为焦点,直线x=-2为准线的抛物线.
设方程为y2=2px,其中
=2,p=4.
所以,动点P的轨迹C的方程为y2=8x.(5分)
(Ⅱ)设过点M的直线方程为x=λy+m,代入y2=8x,得y2-8λy-8m=0.
设A(x1,y1),B(x2,y2),则y1+y2=8λ,y1y2=-8m.
于是x1+x2=λ(y1+y2)+2m=8λ2+2m.
所以AB的中点坐标为(4λ2+m,4λ).
又AB=
=
=
=
.
设存在直线x=x0满足条件,则2|4λ2+m-x0|=
化简,得(16+8x0)λ2+8m-m2-x02+2mx0=0.
所以,(16+8x0)λ2+8m-m2-x02+2mx0=0对任意的λ成立,
所以
,解得x0=-2,m=2.
所以,当m=2时,存在直线x=-2与以线段AB为直径的圆始终相切.(14分)
设方程为y2=2px,其中
| p |
| 2 |
所以,动点P的轨迹C的方程为y2=8x.(5分)
(Ⅱ)设过点M的直线方程为x=λy+m,代入y2=8x,得y2-8λy-8m=0.
设A(x1,y1),B(x2,y2),则y1+y2=8λ,y1y2=-8m.
于是x1+x2=λ(y1+y2)+2m=8λ2+2m.
所以AB的中点坐标为(4λ2+m,4λ).
又AB=
| (x1-x2)2+(y1-y2)2 |
| (1+λ2)(y1-y2)2 |
| (1+λ2)[(y1+y2)2-4y1y2 |
=
| (1+λ2)(64λ2+32m) |
设存在直线x=x0满足条件,则2|4λ2+m-x0|=
| (1+λ2)(64λ2+32m) |
化简,得(16+8x0)λ2+8m-m2-x02+2mx0=0.
所以,(16+8x0)λ2+8m-m2-x02+2mx0=0对任意的λ成立,
所以
|
所以,当m=2时,存在直线x=-2与以线段AB为直径的圆始终相切.(14分)
点评:本题考查抛物线的标准方程,考查直线与抛物线的位置关系,考查学生的计算能力,正确运用韦达定理是关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
某中学进行模拟考试有80个考室,每个考室30个考生,每个考试座位号按1~30号随机抽取试卷进行评分标准,每个考场抽取座位号为15号考生试卷质检,这种抽样方法是( )
| A、简单随机抽样 | B、系统抽样 |
| C、分层抽样 | D、分组抽样 |
下列命题中,真命题是( )
| A、?x0∈R,ex0≤0 | ||||
| B、?x∈R,2x>x2 | ||||
C、双曲线x2-y2=1的离心率为
| ||||
D、双曲线x2-
|
长方体的一条对角线和同一顶点上的三条棱中的两条所成的角为60°、45°,则它和另一条棱所成的角为( )
| A、30° | B、60° |
| C、45° | D、不确定 |
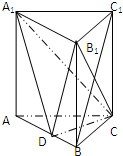 已知直三棱柱ABC-A1B1C1中,AC=BC,点D是AB的中点.
已知直三棱柱ABC-A1B1C1中,AC=BC,点D是AB的中点.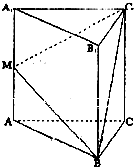 如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,M为AA1中点,求:
如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,M为AA1中点,求: