题目内容
设等比数列{an}的前n项和为Sn,若Sm-1=5,Sm=-11,Sm+1=21,则m=( )
| A、3 | B、4 | C、5 | D、6 |
考点:等比数列的性质
专题:等差数列与等比数列
分析:根据等比数列的通项公式和前n项和公式,建立方程组即可解得m的值.
解答:
解:在等比数列中,
∵Sm-1=5,Sm=-11,Sm+1=21,
∴am=Sm-Sm-1=-11-5=-16,am+1=Sm+1-Sm=21-(-11)=32,
则公比q=
=
=-2,
∵Sm=-11,
∴
=-11,①
又am+1=a1(-2)m=32,②
两式联立解得m=5,a1=-1,
故选:C.
∵Sm-1=5,Sm=-11,Sm+1=21,
∴am=Sm-Sm-1=-11-5=-16,am+1=Sm+1-Sm=21-(-11)=32,
则公比q=
| am+1 |
| am |
| 32 |
| -16 |
∵Sm=-11,
∴
| a1(1-(-2)m) |
| 1+2 |
又am+1=a1(-2)m=32,②
两式联立解得m=5,a1=-1,
故选:C.
点评:本题主要考查等比数列的通项公式和前n项和公式的计算和应用,考查学生的计算能力.

练习册系列答案
相关题目
某中学进行模拟考试有80个考室,每个考室30个考生,每个考试座位号按1~30号随机抽取试卷进行评分标准,每个考场抽取座位号为15号考生试卷质检,这种抽样方法是( )
| A、简单随机抽样 | B、系统抽样 |
| C、分层抽样 | D、分组抽样 |
由200名学生的某次数学考试成绩绘制成了频率分布直方图(如图).由图可知在该次数学考试中成绩小于60分的学生数是( )


| A、600 | B、60 | C、40 | D、4 |
下列命题中,真命题是( )
| A、?x0∈R,ex0≤0 | ||||
| B、?x∈R,2x>x2 | ||||
C、双曲线x2-y2=1的离心率为
| ||||
D、双曲线x2-
|
长方体的一条对角线和同一顶点上的三条棱中的两条所成的角为60°、45°,则它和另一条棱所成的角为( )
| A、30° | B、60° |
| C、45° | D、不确定 |
 已知函数
已知函数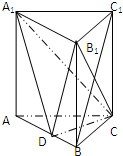 已知直三棱柱ABC-A1B1C1中,AC=BC,点D是AB的中点.
已知直三棱柱ABC-A1B1C1中,AC=BC,点D是AB的中点.