题目内容
曲线y=alnx(a>0)在x=1处的切线与两坐标轴围成的三角形的面积为4,则a= .
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:求出原函数的导函数,得到曲线在x=1处的切线的斜率,由直线方程的点斜式得到切线方程,求出切线在两坐标轴上的截距,由切线与两坐标轴围成的三角形的面积为4列式求得a的值.
解答:
解:由y=alnx,得y′=
,
∴y′|x=1=a,
又x=1时,y=0,
∴曲线y=alnx(a>0)在x=1处的切线方程为:y=ax-a.
当x=0时,y=-a.当y=0时,x=1.
∴切线与两坐标轴围成的三角形的面积等于
×1×a=4.
解得:a=8.
故答案为:8.
| a |
| x |
∴y′|x=1=a,
又x=1时,y=0,
∴曲线y=alnx(a>0)在x=1处的切线方程为:y=ax-a.
当x=0时,y=-a.当y=0时,x=1.
∴切线与两坐标轴围成的三角形的面积等于
| 1 |
| 2 |
解得:a=8.
故答案为:8.
点评:本题考查利用导数研究曲线上某点的切线方程,考查直线方程的点斜式,训练了三角形面积的求法,是中档题.

练习册系列答案
相关题目
长方体的一条对角线和同一顶点上的三条棱中的两条所成的角为60°、45°,则它和另一条棱所成的角为( )
| A、30° | B、60° |
| C、45° | D、不确定 |
已知⊙M经过双曲线S:
-
=1的一个顶点和一个焦点,圆心M在双曲线上S上,则圆心M到双曲线S的中心的距离为( )
| x2 |
| 9 |
| y2 |
| 16 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
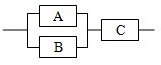 某个部件由三个元件如图方式连接而成,元件A或元件B正常工作,且元件C正常工作,则部件正常工作.若3个元件的次品率均为
某个部件由三个元件如图方式连接而成,元件A或元件B正常工作,且元件C正常工作,则部件正常工作.若3个元件的次品率均为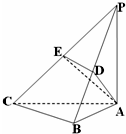 已知三棱锥P-ABC,∠PAC=∠ABC=90°,PA=AC=2BC,平面PAC⊥平面ABC,D、E分别是PB、PC的中点.
已知三棱锥P-ABC,∠PAC=∠ABC=90°,PA=AC=2BC,平面PAC⊥平面ABC,D、E分别是PB、PC的中点.