题目内容
已知圆C1:(x+3)2+y2=1和圆C2:(x-3)2+y2=9,动圆M同时与圆C1及圆C2相外切,则动圆圆心M的轨迹方程是( )
A、x2-
| ||||
B、
| ||||
C、x2+
| ||||
D、
|
考点:圆与圆的位置关系及其判定
专题:直线与圆
分析:设动圆圆心M的坐标为(x,y),半径为r,由题意可得|MC2|-|MC1|=2<|C1C2|,可得点M的轨迹是以C1、C2 为焦点的双曲线的左支.根据2a=2,c=3,求得b=
的值,可得点M的轨迹方程.
| c2-a2 |
解答:
解:设动圆圆心M的坐标为(x,y),半径为r,
则由题意可得|MC1|=r+1,|MC2|=r+3,相减可得|MC2|-|MC1|=2<|C1C2|,
故点M的轨迹是以C1、C2 为焦点的双曲线的左支.
由题意可得 2a=2,c=3,∴b=
=2
,
故点M的轨迹方程为 x2-
=1(x≤-1),
故选:A.
则由题意可得|MC1|=r+1,|MC2|=r+3,相减可得|MC2|-|MC1|=2<|C1C2|,
故点M的轨迹是以C1、C2 为焦点的双曲线的左支.
由题意可得 2a=2,c=3,∴b=
| c2-a2 |
| 2 |
故点M的轨迹方程为 x2-
| y2 |
| 8 |
故选:A.
点评:本题主要考查两圆向外切的性质,双曲线的定义、性质和标准方程,属于基础题.

练习册系列答案
相关题目
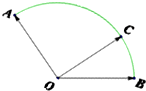 如图,在圆心角为120°的扇形中,以圆心O为起点作射线OC,则使得∠AOC与∠BOC都不大于90°的概率是( )
如图,在圆心角为120°的扇形中,以圆心O为起点作射线OC,则使得∠AOC与∠BOC都不大于90°的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
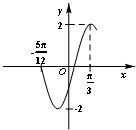 函数f(x)=2sin(ωx+φ)(ω>0,-
函数f(x)=2sin(ωx+φ)(ω>0,-| π |
| 2 |
| π |
| 2 |
A、2,-
| ||
B、4,
| ||
C、4,-
| ||
D、2,-
|
△ABC中,a=x,b=2,∠B=60°,则当△ABC有两个解时,x的取值范围是( )
A、x>
| ||||
B、x<2或x>
| ||||
| C、x<2 | ||||
D、2<x<
|
设X为随机变量,X~B(n,
),若随机变量X的方差D(X)=1,则P(X=2)等于( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
