题目内容
求不等式
≤0的解集是 ．
| x2-x+2 |
| x2-x+1 |
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：因为x2-x+1＞0恒成立，所以不等式等价转化为x2-x+2≤0，然后解之．
解答：
解：∵x2-x+1＞0恒成立
∴不等式
≤0?x2-x+2≤0，判别式△=1-8=-7＜0，
∴x2-x+2≤0的解集为∅；
故答案为：∅
∴不等式
| x2-x+2 |
| x2-x+1 |
∴x2-x+2≤0的解集为∅；
故答案为：∅
点评：本题考查了分式不等式、一元二次不等式的解法；本题关键是正确转化为一元二次不等式解答．
练习册系列答案
阅读快车系列答案
相关题目
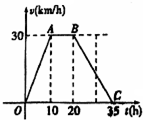据气象中心观察和预测：发生于沿海M地的台风一直想正南方向移动，其运动速度v（km/h）与时间t（h）的函数图象如图所示，过线段OC上一点T（t，0）作横轴的垂下l，梯形OABC在直线l左侧部分的面积即为t（h）内台风所经过的路程s（km）数列{3n2-28n}中，各项中最小的项是（ ）
| A、第4项 | B、第5项 |
| C、第6项 | D、第7项 |
已知向量
，
满足
=1，
=2，
•
=-
，则
与
的夹角为（ ）
| a |
| b |
| |a| |
| |b| |
| a |
| b |
| 3 |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|