题目内容
函数f(x)=sin(ωx+φ)(A>0,ω>0,-π<φ<0),y=f(x)的周期为π,其图象最高点(
,1).
(1)求该函数的解析式;
(2)用“五点法”画出函数y=f(x)在区间[0,π]上的图象;
(3)方程f(x)=a在[
,
]上有两个相异的根x1、x2,求x1+x2的值.
| 5π |
| 8 |
(1)求该函数的解析式;
(2)用“五点法”画出函数y=f(x)在区间[0,π]上的图象;
(3)方程f(x)=a在[
| 3π |
| 8 |
| 7π |
| 8 |
考点:五点法作函数y=Asin(ωx+φ)的图象,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)根据三角函数的图象即可求y=f(x)的解析式;
(2)根据“五点法”即可画出函数在长度为一个周期的闭区间上的简图;
(3)根据三角函数图象之间的关系,即可得到结论.
(2)根据“五点法”即可画出函数在长度为一个周期的闭区间上的简图;
(3)根据三角函数图象之间的关系,即可得到结论.
解答:
 解:(1)∵y=f(x)的周期为π,
解:(1)∵y=f(x)的周期为π,
∴T=
=π,
则ω=2,
又函数图象最高点(
,1).
∴f(
)=1,
即sin(
+φ)=1.
∵-π<φ<0,
∴
+φ∈(
,
),
即
+φ=
,
解得φ=-
,
则y=f(x)的解析式为f(x)=sin(2x-
).
(2)由f(x)=sin(2x-
)得
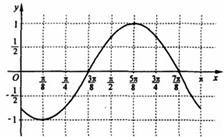
故函数的图象如右图:
(3)若f(x)=a在[
,
]上有两个相异的根x1、x2,
则两个相异的根x1、x2,关于x=
对称,
即x1+x2=
.
 解:(1)∵y=f(x)的周期为π,
解:(1)∵y=f(x)的周期为π,∴T=
| 2π |
| ω |
则ω=2,
又函数图象最高点(
| 5π |
| 8 |
∴f(
| 5π |
| 8 |
即sin(
| 5π |
| 8 |
∵-π<φ<0,
∴
| 5π |
| 8 |
| π |
| 4 |
| 5π |
| 4 |
即
| 5π |
| 8 |
| π |
| 2 |
解得φ=-
| 3π |
| 4 |
则y=f(x)的解析式为f(x)=sin(2x-
| 3π |
| 4 |
(2)由f(x)=sin(2x-
| 3π |
| 4 |
| x | 0 |
|
|
|
| π | ||||||||
| y | -
| -1 | 0 | 1 | 0 | -
|
(3)若f(x)=a在[
| 3π |
| 8 |
| 7π |
| 8 |
则两个相异的根x1、x2,关于x=
| 5π |
| 8 |
即x1+x2=
| 5π |
| 4 |
点评:本题主要考查三角函数的图象和性质,要求熟练掌握三角函数的图象,单调性,最值性质的求解和应用.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
在△ABC中,若c2=a2+b2+ab,则△ABC是( )
| A、等边三角形 |
| B、锐角三角形 |
| C、直角三角形 |
| D、钝角三角形 |