题目内容
3.已知椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$和圆${C_2}:{x^2}+{y^2}={b^2}$,若椭圆C1上存在点P,过点P作圆C2的两条切线PA,PB(A,B为对应的切点),且满足$∠APB=\frac{π}{3}$,则椭圆最圆的时离心率e=( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{2}}}{4}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
分析 连接OA,OB,OP,依题意,O、P、A、B四点共圆,可得∠APB=60°,∠APO=∠BPO=30°,在直角三角形OAP中,∠AOP=60°,cos∠AOP=$\frac{b}{|OP|}$=$\frac{1}{2}$,可得b<|OP|≤a,可得椭圆C的离心率的取值范围.
解答 解:连接OA,OB,OP,依题意,O、P、A、B四点共圆,
∵∠APB=60°,
∠APO=∠BPO=30°,
在直角三角形OAP中,∠AOP=60°,
∴cos∠AOP=$\frac{b}{|OP|}$=$\frac{1}{2}$,
∴|OP|=2b,
∴b<|OP|≤a,
∴2b≤a,
∴4b2≤a2,
由a2=b2+c2,即4(a2-c2)≤a2,
∴3a2≤4c2,
即e≥$\frac{\sqrt{3}}{2}$,又0<e<1,
∴$\frac{\sqrt{3}}{2}$≤e<1,
∴椭圆C的离心率的取值范围是$\frac{\sqrt{3}}{2}$≤e<1.
∴椭圆最圆的时离心率e=$\frac{\sqrt{3}}{2}$.
故选:C.
点评 本题考查了椭圆的标准方程及其性质、四点共圆的性质、直角三角形的边角关系、不等式的性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
13.在区间[0,2]上随机地取一个数x,则事件“-1≤log ${\;}_{\frac{1}{2}}$(x+$\frac{1}{2}$)≤1”发生的概率( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
8.若变量x,y满足约束条件$\left\{\begin{array}{l}x≥0\\ y≥0\\ x+y≤8\\ 2y-x≤4\end{array}\right.$,且z=5y-x的最大值为a,最小值为b,则a-b的值是( )
| A. | 16 | B. | 24 | C. | 30 | D. | 48 |
15.函数y=Asin(ωx+ϕ)$(ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,则函数表达式为( )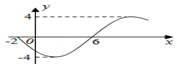

| A. | $y=-4sin(\frac{π}{8}x-\frac{π}{4})$ | B. | $y=4sin(\frac{π}{8}x-\frac{π}{4})$ | C. | $y=-4sin(\frac{π}{8}x+\frac{π}{4})$ | D. | $y=4sin(\frac{π}{8}x+\frac{π}{4})$ |