题目内容
3.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{4}(x+1)+x-1(x>0)}\\{x-(\frac{1}{4})^{x+1}+3(x≤0)}\end{array}\right.$,若f(x)的两个零点分别为x1,x2,则|x1-x2|=( )| A. | $\sqrt{2}$ | B. | 1+$\frac{\sqrt{2}}{2}$ | C. | 2 | D. | $\frac{3}{2}$+ln2 |
分析 由题意分别讨论两段函数的零点,转化为两个函数图象交点的横坐标,然后结合互为反函数图象的对称性及图象平移求解.
解答 解:当x>0时,f(x)=log4(x+1)+x-1,
由f(x)=0,可得x-1=$-lo{g}_{4}(x+1)=lo{g}_{\frac{1}{4}}(x+1)$;
当x≤0时,f(x)=x-$(\frac{1}{4})^{x+1}$+3,
由f(x)=0,可得$(\frac{1}{4})^{x+1}=x+3$.
作出函数图象如图:
∵函数y=$lo{g}_{\frac{1}{4}}x$与y=$(\frac{1}{4})^{x}$互为反函数,则其图象关于直线y=x对称,
而$y=lo{g}_{\frac{1}{4}}(x+1)$与$y=(\frac{1}{4})^{x+1}$分别是把y=$lo{g}_{\frac{1}{4}}x$与y=$(\frac{1}{4})^{x}$向左平移1个单位得到的,
∴两函数图象关于直线y=x+1对称,
又直线y=x-1与y=x+3也关于直线y=x+1对称,
不妨设y=x+3(x≤0)与y=$(\frac{1}{4})^{x+1}$的交点的横坐标为x1,y=x-1(x>0)与y=$lo{g}_{\frac{1}{4}}(x+1)$的交点的横坐标为x2,
则|x1-x2|=$\frac{|AB|}{2}=\frac{4}{2}=2$.
故选:C.
点评 本题考查分段函数的应用,考查根的存在性与根的个数判断,考查数学转化思想方法与数形结合的解题思想方法,是中档题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
8.已知集合M={x|x2-1≤0},N=|x∈Z|$\frac{1}{2}$<2x+1<4},则M∩N=( )
| A. | {1} | B. | {-1,0} | C. | {-1,0,1} | D. | ∅ |
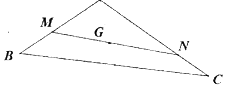 如图,已知点G是△ABC的重心,过点G作直线与AB、AC两边分别交于M、N两点,且$\overrightarrow{AM}$=$\frac{a}{3}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{b}{6}$$\overrightarrow{AC}$,则$\frac{2}{a-1}$+$\frac{1}{b-2}$的最小值为3.
如图,已知点G是△ABC的重心,过点G作直线与AB、AC两边分别交于M、N两点,且$\overrightarrow{AM}$=$\frac{a}{3}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{b}{6}$$\overrightarrow{AC}$,则$\frac{2}{a-1}$+$\frac{1}{b-2}$的最小值为3.