题目内容
11.等差数列{an}中a2=5,a6=21.(1)求{an}的通项公式及前n项和Sn;
(2)设${b_n}=\frac{2}{{{S_n}+5n}}$,求数列{bn}的前n项和Tn.
分析 (1)设{an}的公差为d,由等差数列的通项公式,可得首项和公差的方程,即可得到所求通项公式和前n项和Sn;
(2)求得${b_n}=\frac{2}{{{S_n}+5n}}$=$\frac{2}{2{n}^{2}-n+5n}$=$\frac{1}{{n}^{2}+2n}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),运用数列的求和方法:裂项相消求和,化简整理即可得到所求和.
解答 解:(1)设{an}的公差为d,
由a2=5,a6=21,
即为a1+d=5,a1+5d=21,
解得d=4,a1=1
可得{an}的通项公式an=a1+(n-1)d=1+4(n-1)=4n-3,
Sn=$\frac{n(1+4n-3)}{2}$=n(2n-1);
(2)${b_n}=\frac{2}{{{S_n}+5n}}$=$\frac{2}{2{n}^{2}-n+5n}$=$\frac{1}{{n}^{2}+2n}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),
则数列{bn}的前n项和Tn=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{n}$-$\frac{1}{n+2}$)
=$\frac{1}{2}$(1+$\frac{1}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$)=$\frac{3}{4}$-$\frac{1}{2n+2}$-$\frac{1}{2n+4}$.
点评 本题考查等差数列的通项公式和求和公式,注意运用方程思想,考查数列的求和方法:裂项相消求和,考查化简整理的运算能力,属于中档题.

| A. | 若(a-2)(b-3)≠0,则a≠2或b≠3 | B. | 若(a-2)(b-3)≠0,则a≠2且b≠3 | ||
| C. | 若(a-2)(b-3)=0,则a≠2或b≠3 | D. | 若(a-2)(b-3)=0,则a≠2且b≠3 |
| A. | [3,4] | B. | [4,7] | C. | [3,7] | D. | [1,7] |
| A. | $\frac{4}{3}π$ | B. | $\frac{8}{3}π$ | C. | $\frac{10}{3}π$ | D. | $\frac{16}{3}π$ |
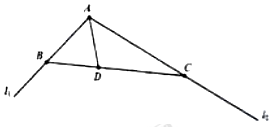 某市渭河的某水域有夹角为120°的两条直线河岸l1,l2(如图所示):在该水域中,位于该角平分线且距A地相距1公里的D处有座千年古亭,为保护古亭,沿D所在直线BC建一河堤(B,C分别在l1,l2上,河堤下方有进、出水的桥洞);现要在△ABC水域建一个水上游乐城,如何设计AB、AC河岸的长度,AB、AC都不超过5公里(不妨令AB=x公里,AC=y公里).
某市渭河的某水域有夹角为120°的两条直线河岸l1,l2(如图所示):在该水域中,位于该角平分线且距A地相距1公里的D处有座千年古亭,为保护古亭,沿D所在直线BC建一河堤(B,C分别在l1,l2上,河堤下方有进、出水的桥洞);现要在△ABC水域建一个水上游乐城,如何设计AB、AC河岸的长度,AB、AC都不超过5公里(不妨令AB=x公里,AC=y公里).