题目内容
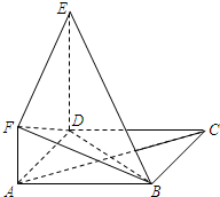 如图,正方形ABCD与直角梯形ADEF所在平面互相垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2
如图,正方形ABCD与直角梯形ADEF所在平面互相垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2(1)求证:AC∥平面BEF;
(2)求点D到平面BEF的距离;
(3)求平面BEF与平面ABCD所成的正切值.
考点:用空间向量求平面间的夹角,直线与平面平行的判定,与二面角有关的立体几何综合题,点、线、面间的距离计算
专题:空间位置关系与距离,空间向量及应用
分析:(1)设AC∩BD=O,取BE中点G,连接FG,OG,由已知条件推导出四边形AFGO是平行四边形,由此能够证明AC∥平面BEF.
(2)以D为原点,以DA为x轴,以DC为y轴,以DE为z轴,建立空间直角坐标系,利用向量法能求出点D到平面BEF的距离.
(3)分别求出平面ABCD的法向量和平面BEF的法向量,利用向量法能结合三角函数知识能求出平面BEF与平面ABCD所成角的正切值.
(2)以D为原点,以DA为x轴,以DC为y轴,以DE为z轴,建立空间直角坐标系,利用向量法能求出点D到平面BEF的距离.
(3)分别求出平面ABCD的法向量和平面BEF的法向量,利用向量法能结合三角函数知识能求出平面BEF与平面ABCD所成角的正切值.
解答:
(1)证明:设AC∩BD=O,取BE中点G,连接FG,OG,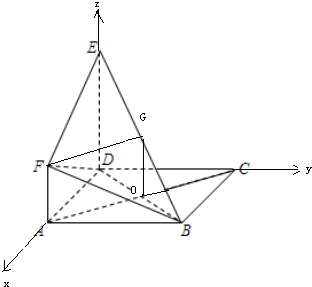
∴OG∥DE,且OG=
DE.
∵AF∥DE,DE=2AF,
∴AF∥OG,且OG=AF,
∴四边形AFGO是平行四边形,FG∥OA.
∴FG?平面BEF,AO?平面BEF,
∴AO∥平面BEF,即AC∥平面BEF.…(6分)
(2)解:∵正方形ABCD与直角梯形ADEF所在平面互相垂直,
∠ADE=90°,
∴以D为原点,以DA为x轴,以DC为y轴,以DE为z轴,建立空间直角坐标系,
∵DE=DA=2AF=2,
∴B(2,2,0),E(0,0,2),F(2,0,1),D(0,0,0),
∴
=(-2,-2,2),
=(0,-2,1),
=(-2,-2,0),
设平面BEF的法向量
=(x,y,z),则
•
=0,
•
=0,
∴
,∴
=(1,1,2),
∴点D到平面BEF的距离d=
=
=
.
(3)解:设平面BEF与平面ABCD所成的角为θ
∵平面ABCD的法向量
=(0,0,1),
平面BEF的法向量
=(1,1,2),
∴cosθ=|cos<
,
>|=|
|=
,
∴sinθ=
=
,
∴tanθ=
=
.
∴平面BEF与平面ABCD所成角的正切值为
.

∴OG∥DE,且OG=
| 1 |
| 2 |
∵AF∥DE,DE=2AF,
∴AF∥OG,且OG=AF,
∴四边形AFGO是平行四边形,FG∥OA.
∴FG?平面BEF,AO?平面BEF,
∴AO∥平面BEF,即AC∥平面BEF.…(6分)
(2)解:∵正方形ABCD与直角梯形ADEF所在平面互相垂直,
∠ADE=90°,
∴以D为原点,以DA为x轴,以DC为y轴,以DE为z轴,建立空间直角坐标系,
∵DE=DA=2AF=2,
∴B(2,2,0),E(0,0,2),F(2,0,1),D(0,0,0),
∴
| BE |
| BF |
| BD |
设平面BEF的法向量
| n |
| n |
| BE |
| n |
| BF |
∴
|
| n |
∴点D到平面BEF的距离d=
|
| ||||
|
|
| |-2-2+0| | ||
|
2
| ||
| 3 |
(3)解:设平面BEF与平面ABCD所成的角为θ
∵平面ABCD的法向量
| m |
平面BEF的法向量
| n |
∴cosθ=|cos<
| m |
| n |
| 2 | ||
|
| ||
| 3 |
∴sinθ=
1-(
|
| ||
| 3 |
∴tanθ=
| sinθ |
| cosθ |
| ||
| 2 |
∴平面BEF与平面ABCD所成角的正切值为
| ||
| 2 |
点评:本题考查直线与平面平行的证明,考查点到平面的距离的求法,考查平面与平面所成角的正切值的求法,解题时要注意向量法的合理运用.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
下列说法中错误的是( )
| A、对于命题p:x0∈R,sin x0>1,则¬p:x∈R,sin x≤1 |
| B、命题“若0<a<1,则函数f(x)=ax在R上是增函数”的逆命题为假命题 |
| C、若p∨q为真命题,则p,q均为真命题 |
| D、命题“若x2-x-2=0,则x=2”的逆否命题是“若x≠2,则x2-x-2≠0” |
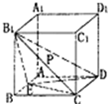 如图,正方体ABCD-A1B1C1D1的棱长为1,E是AB的中点,P是B1C的中点.
如图,正方体ABCD-A1B1C1D1的棱长为1,E是AB的中点,P是B1C的中点.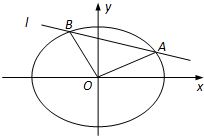 在平面直角坐标系xOy中,设椭圆C的中心在原点,焦点在x轴上,短半轴长为2,椭圆C长轴的右端点到其右焦点的距离为
在平面直角坐标系xOy中,设椭圆C的中心在原点,焦点在x轴上,短半轴长为2,椭圆C长轴的右端点到其右焦点的距离为