题目内容
给出命题:p:3≥3,q:函数f(x)=
在R上是连续函数,则在下列三个复合命题:
①“p∧q”;
②“p∨q”;
③“¬p”,
其中真命题的个数为 .
|
①“p∧q”;
②“p∨q”;
③“¬p”,
其中真命题的个数为
考点:命题的真假判断与应用
专题:简易逻辑
分析:由命题:p:3≥3,可知命题P正确;对于命题:q:函数f(x)=
在R上是连续函数,由于当x=0时,函数f(x)不连续,因此函数在R上不是连续函数,即可判断出q是假命题.再利用“或且非”命题真假的判断方法即可得出.
|
解答:
解:由命题:p:3≥3,可知命题P是真命题;
对于命题:q:函数f(x)=
在R上是连续函数,由于当x=0时,函数f(x)不连续,因此函数在R上不是连续函数.
据此可知:①“p∧q”是假命题;
②“p∨q”是真命题;
③“¬p”是假命题.
综上可知:只有②是真命题.
故真命题的个数为1.
故答案为:1.
对于命题:q:函数f(x)=
|
据此可知:①“p∧q”是假命题;
②“p∨q”是真命题;
③“¬p”是假命题.
综上可知:只有②是真命题.
故真命题的个数为1.
故答案为:1.
点评:本题考查了“或且非”命题真假的判断方法,属于基础题.

练习册系列答案
相关题目
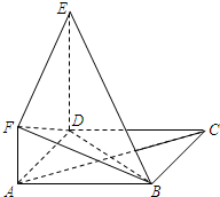 如图,正方形ABCD与直角梯形ADEF所在平面互相垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2
如图,正方形ABCD与直角梯形ADEF所在平面互相垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2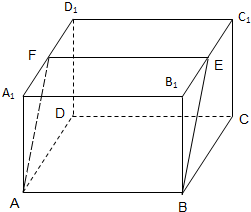 如图,直四棱柱ABCD-A1B1C1D1的底面边长为2的菱形,∠BAD=60°,高为1,过底边AB作一截面ABEF,若BE=2
如图,直四棱柱ABCD-A1B1C1D1的底面边长为2的菱形,∠BAD=60°,高为1,过底边AB作一截面ABEF,若BE=2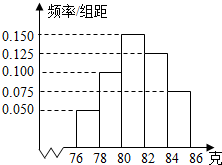 某厂对一批产品进行抽样检测,图2是抽检产品净重(单位:克)数据的频率分布直方图,样本数据分组为[76,78)、[78,80)、…、[84,86].若这批产品有120个,估计其中净重大于或等于78克且小于84克的产品的个数是
某厂对一批产品进行抽样检测,图2是抽检产品净重(单位:克)数据的频率分布直方图,样本数据分组为[76,78)、[78,80)、…、[84,86].若这批产品有120个,估计其中净重大于或等于78克且小于84克的产品的个数是 如图,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,平面PAB⊥平面ABCD,PA=PB=2AB.
如图,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,平面PAB⊥平面ABCD,PA=PB=2AB.